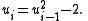Lucas-Lehmer-Riesel test
Encyclopedia
In mathematics, the Lucas–Lehmer–Riesel test is a primality test
for numbers of the form N = k2n − 1, with 2n > k. The test was developed by Hans Riesel
and it is based on the Lucas–Lehmer primality test. It is the fastest deterministic algorithm known for numbers of that form. The Brillhart–Lehmer–Selfridge test is the fastest deterministic algorithm for numbers of the form N = k2n + 1
Define a sequence {ui} for all i > 0 by:
Then N is prime if and only if it divides un−2.
For Lucas-style tests on a number N, we work in the multiplicative group of a quadratic extension of the integers modulo N; if N is prime, the order of this multiplicative group is N2 − 1, it has a subgroup of order N + 1, and we try to find a generator for that subgroup.
We start off by trying to find a non-iterative expression for the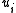
. Following the model of the Lucas–Lehmer test, put 
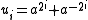, and by induction we have 
.
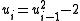So we can consider ourselves as looking at the 2ith term of the sequence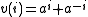
. If a satisfies a quadratic equation, this is a Lucas sequence, and has an expression of the form 
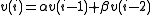. Really, we're looking at the 
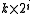th term of a different sequence, but since decimations (take every kth term starting with the zeroth) of a Lucas sequence are themselves Lucas sequences, we can deal with the factor k by picking a different starting point.
projects including Riesel Sieve
and PrimeGrid
.
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
for numbers of the form N = k2n − 1, with 2n > k. The test was developed by Hans Riesel
Hans Riesel
Hans Ivar Riesel is a Swedish mathematician who discovered the 18th known Mersenne prime in 1957, using the computer BESK. This prime is 23217-1, which consists of 969 digits. He held the record for the largest known prime from 1957 to 1961, when Alexander Hurwitz discovered a larger one. Riesel...
and it is based on the Lucas–Lehmer primality test. It is the fastest deterministic algorithm known for numbers of that form. The Brillhart–Lehmer–Selfridge test is the fastest deterministic algorithm for numbers of the form N = k2n + 1
The algorithm
The algorithm is very similar to the Lucas–Lehmer test, but with a variable starting point depending on the value of k.Define a sequence {ui} for all i > 0 by:
Then N is prime if and only if it divides un−2.
Finding the starting value
- If
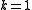: if n is odd, then we can take u0 = 4. If n = 3 mod 4, then we can take 
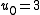. Note that if n is prime, these are Mersenne numbers. - If
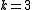: if n = 0 or 3 mod 4 then 
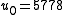. - If k = 1 or 5 mod 6 and 3 does not divide N, then we take
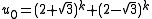. - Otherwise, we are in the case where k is a multiple of 3, and it is more difficult to select the right value of
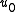
How does the test work?
The Lucas–Lehmer–Riesel test is a particular case of group-order primality testing; we demonstrate that some number is prime by showing that some group has the order that it would have were that number prime, and we do this by finding an element of that group of precisely the right order.For Lucas-style tests on a number N, we work in the multiplicative group of a quadratic extension of the integers modulo N; if N is prime, the order of this multiplicative group is N2 − 1, it has a subgroup of order N + 1, and we try to find a generator for that subgroup.
We start off by trying to find a non-iterative expression for the
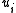. Following the model of the Lucas–Lehmer test, put 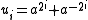, and by induction we have 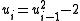.So we can consider ourselves as looking at the 2ith term of the sequence
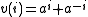. If a satisfies a quadratic equation, this is a Lucas sequence, and has an expression of the form 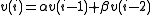. Really, we're looking at the 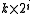th term of a different sequence, but since decimations (take every kth term starting with the zeroth) of a Lucas sequence are themselves Lucas sequences, we can deal with the factor k by picking a different starting point.LLR software
LLR is a program that can run the LLR tests. The program was developed by Jean Penné. Vincent Penné has modified the program so that it can obtain tests via the Internet. The software is both used by individual prime searchers and some distributed computingDistributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
projects including Riesel Sieve
Riesel Sieve
Riesel Sieve is a distributed computing project, running in part on the BOINC platform. Its aim is to prove that is the smallest Riesel number, by finding a prime of the form for all odd smaller than .-Progress of the project:...
and PrimeGrid
PrimeGrid
PrimeGrid is a distributed computing project for searching for prime numbers of world-record size. It makes use of the Berkeley Open Infrastructure for Network Computing platform...
.