
M-tree
Encyclopedia
M-trees are tree data structures that are similar to R-tree
s and B-tree
s. It is constructed using a metric
and relies on the triangle inequality
for efficient range and k-NN queries.
While M-trees can perform well in many conditions, the tree can also have large overlap and there is no clear strategy on how to best avoid overlap. In addition, it can only be used for distance functions that satisfy the triangle inequality, while many advanced dissimilarity functions used in information retrieval
do not satisfy this.
 and leaf
and leaf 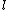 residing in a particular node
residing in a particular node 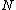 is at most distance
is at most distance  from
from 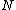 , and every node n and leaf l with node parent N keep the distance from it.
, and every node n and leaf l with node parent N keep the distance from it.
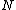 where the new object
where the new object 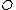 belongs. If
belongs. If 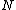 is not full then just attach it to
is not full then just attach it to 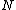 . If
. If 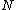 is full then invoke a method to split
is full then invoke a method to split 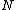 . The algorithm is as follows:
. The algorithm is as follows:
Input: Node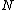 of M-Tree
of M-Tree 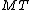 , Entry
, Entry 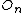
Output: A new instance of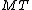 containing all entries in original
containing all entries in original 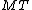 plus
plus 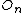
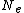 ← Entries of node
← Entries of node 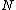
if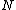 is not a leaf then
is not a leaf then
{
/*Look for entries that the new object fits into*/
let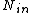 be entries such that
be entries such that 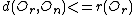
if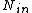 is not empty then
is not empty then
{
/*If there are one or more entry, then look for an entry such that is closer to the new object*/
let be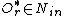 such that
such that 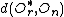 is minimum
is minimum
}
else
{
/*If there are no such entry, then look for an entry with minimal distance from its edge to the new object*/
let be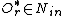 such that
such that 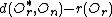 is minimum
is minimum
/*Upgrade the new radii of the entry*/
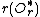 =
= 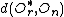
}
/*Continue inserting in the next level*/
return insert(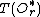 ,
, 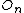 );
);
else
{
/*If the node has capacity then just insert the new object*/
if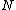 is not full then
is not full then
{ store(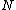 ,
, 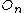 ) }
) }
/*The node is at full capacity, then it is needed to do a new split in this level*/
else
{ split(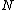 ,
, 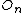 ) }
) }
}
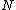 , and creates two new nodes containing all the objects in original
, and creates two new nodes containing all the objects in original 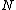 , and store them into the new root. If split methods arrives to a node
, and store them into the new root. If split methods arrives to a node 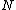 that is not the root of the tree, the method choose two new routing objects from
that is not the root of the tree, the method choose two new routing objects from 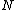 , re-arrange every routing object in
, re-arrange every routing object in 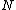 in two new nodes
in two new nodes 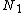 and
and 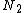 , and store this new nodes in the parent node
, and store this new nodes in the parent node 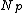 of original
of original 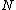 . The split must be repeated if
. The split must be repeated if 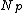 has not enough capacity to store
has not enough capacity to store 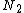 . The algorithm is as follow:
. The algorithm is as follow:
Input: Node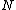 of M-Tree
of M-Tree 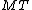 , Entry
, Entry 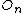
Output: A new instance of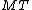 containing a new partition.
containing a new partition.
/*The new routing objects are now all those in the node plus the new routing object*/
let be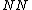 entries of
entries of 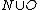
if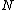 is not the root then
is not the root then
{
/*Get the parent node and the parent routing object*/
let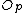 be the parent routing object of
be the parent routing object of 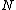
let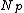 be the parent node of
be the parent node of 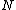
}
/*This node will contain part of the objects of the node to be split*/
Create a new node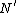
/*Promote two routing objects from the node to be split, to be new routing objects*/
Promote(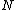 ,
, 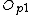 ,
, 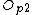 )
)
/*Choose which objects from the node being split will act as new routing objects*/
Partition(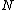 ,
, 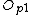 ,
, 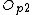 ,
, 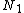 ,
, 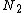 )
)
/*Store entries in each new routing object*/
Store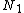 's entries in
's entries in 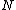 and
and 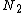 's entries in
's entries in 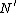
if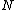 is the current root then
is the current root then
{
/*Create a new node and set it as new root and store the new routing objects*/
Create a new root node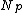
Store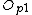 and
and 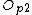 in
in 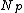
}
else
{
/*Now use the parent rouing object to store one of the new objects*/
Replace entry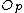 with entry
with entry 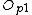 in
in 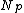
if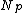 is no full then
is no full then
{
/*The second routinb object is stored in the parent only if it has free capacity*/
Store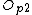 in
in 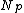
}
else
{
/*If there is no free capacity then split the level up*/
split(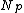 ,
, 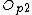 )
)
}
}
R-tree
R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984 and has found significant use in both research and real-world applications...
s and B-tree
B-tree
In computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children...
s. It is constructed using a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
and relies on the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
for efficient range and k-NN queries.
While M-trees can perform well in many conditions, the tree can also have large overlap and there is no clear strategy on how to best avoid overlap. In addition, it can only be used for distance functions that satisfy the triangle inequality, while many advanced dissimilarity functions used in information retrieval
Information retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
do not satisfy this.
Overview
As in any Tree-based data structure, the M-Tree is composed of Nodes and Leaves. In each node there is a data object that identifies it uniquely and a pointer to a sub-tree where its children reside. Every leaf has several data objects. For each node there is a radius r that defines a Ball in the desired metric space. Thus, every node and leaf
and leaf 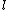 residing in a particular node
residing in a particular node 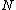 is at most distance
is at most distance  from
from 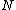 , and every node n and leaf l with node parent N keep the distance from it.
, and every node n and leaf l with node parent N keep the distance from it.Components
An M-Tree has these components and sub-components:- Root.
- Routing object O.
- Radius Or.
- A set of Nodes or (exclusive) Leafs.
- Node.
- Routing object Or.
- Radius Or.
- Distance from this node to its parent Op.
- A set of Nodes or (exclusive) Leafs.
- Leaf.
- Routing object O.
- Radius Or.
- Distance from this leaf to its parent Op.
- Objects.
- Objects.
- Feature value (usually a d-dimensional vector).
Insert
The main idea is first to find a leaf node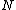 where the new object
where the new object 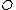 belongs. If
belongs. If 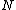 is not full then just attach it to
is not full then just attach it to 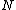 . If
. If 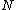 is full then invoke a method to split
is full then invoke a method to split 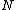 . The algorithm is as follows:
. The algorithm is as follows:Input: Node
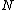 of M-Tree
of M-Tree 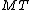 , Entry
, Entry 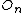
Output: A new instance of
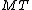 containing all entries in original
containing all entries in original 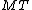 plus
plus 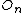
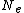 ← Entries of node
← Entries of node 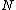
if
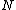 is not a leaf then
is not a leaf then{
/*Look for entries that the new object fits into*/
let
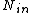 be entries such that
be entries such that 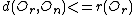
if
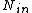 is not empty then
is not empty then{
/*If there are one or more entry, then look for an entry such that is closer to the new object*/
let be
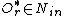 such that
such that 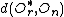 is minimum
is minimum}
else
{
/*If there are no such entry, then look for an entry with minimal distance from its edge to the new object*/
let be
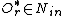 such that
such that 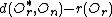 is minimum
is minimum/*Upgrade the new radii of the entry*/
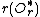 =
= 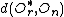
}
/*Continue inserting in the next level*/
return insert(
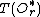 ,
, 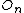 );
);else
{
/*If the node has capacity then just insert the new object*/
if
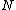 is not full then
is not full then{ store(
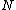 ,
, 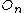 ) }
) }/*The node is at full capacity, then it is needed to do a new split in this level*/
else
{ split(
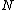 ,
, 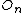 ) }
) }}
Split
If the split method arrives to the root of the tree, then it choose two routing objects from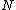 , and creates two new nodes containing all the objects in original
, and creates two new nodes containing all the objects in original 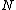 , and store them into the new root. If split methods arrives to a node
, and store them into the new root. If split methods arrives to a node 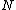 that is not the root of the tree, the method choose two new routing objects from
that is not the root of the tree, the method choose two new routing objects from 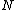 , re-arrange every routing object in
, re-arrange every routing object in 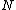 in two new nodes
in two new nodes 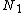 and
and 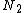 , and store this new nodes in the parent node
, and store this new nodes in the parent node 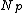 of original
of original 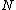 . The split must be repeated if
. The split must be repeated if 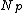 has not enough capacity to store
has not enough capacity to store 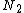 . The algorithm is as follow:
. The algorithm is as follow:Input: Node
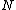 of M-Tree
of M-Tree 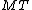 , Entry
, Entry 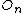
Output: A new instance of
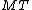 containing a new partition.
containing a new partition./*The new routing objects are now all those in the node plus the new routing object*/
let be
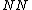 entries of
entries of 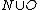
if
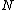 is not the root then
is not the root then{
/*Get the parent node and the parent routing object*/
let
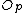 be the parent routing object of
be the parent routing object of 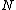
let
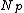 be the parent node of
be the parent node of 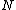
}
/*This node will contain part of the objects of the node to be split*/
Create a new node
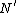
/*Promote two routing objects from the node to be split, to be new routing objects*/
Promote(
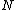 ,
, 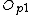 ,
, 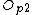 )
)/*Choose which objects from the node being split will act as new routing objects*/
Partition(
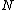 ,
, 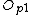 ,
, 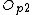 ,
, 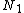 ,
, 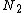 )
)/*Store entries in each new routing object*/
Store
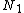 's entries in
's entries in 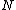 and
and 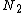 's entries in
's entries in 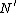
if
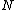 is the current root then
is the current root then{
/*Create a new node and set it as new root and store the new routing objects*/
Create a new root node
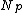
Store
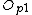 and
and 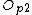 in
in 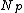
}
else
{
/*Now use the parent rouing object to store one of the new objects*/
Replace entry
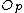 with entry
with entry 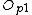 in
in 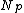
if
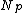 is no full then
is no full then{
/*The second routinb object is stored in the parent only if it has free capacity*/
Store
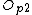 in
in 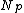
}
else
{
/*If there is no free capacity then split the level up*/
split(
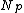 ,
, 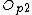 )
)}
}
See also
- Segment treeSegment treeIn computer science, a segment tree is a tree data structure for storing intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, its content cannot be modified once the structure is built...
- Interval treeInterval treeIn computer science, an interval tree is an ordered tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for example, to find all roads on a computerized map inside...
- A degenerate R-Tree for 1 dimension (usually time). - Bounding volume hierarchyBounding volume hierarchyA bounding volume hierarchy is a tree structure on a set of geometric objects. All geometric objects are wrapped in bounding volumes that form the leaf nodes of the tree. These nodes are then grouped as small sets and enclosed within larger bounding volumes...
- Spatial index
- GiSTGiSTIn computing, GiST or Generalized Search Tree, is a data structure and API that can be used to build a variety of disk-based search trees. GiST is a generalization of the B+ tree, providing a concurrent and recoverable height-balanced search tree infrastructure without making any assumptions about...

