
Malleability (cryptography)
Encyclopedia
Malleability is a property of some cryptographic
algorithm
s. An encryption algorithm is malleable if it is possible for an adversary to transform a ciphertext
into another ciphertext which decrypts to a related plaintext
. That is, given an encryption of a plaintext , it is possible to generate another ciphertext which decrypts to
, it is possible to generate another ciphertext which decrypts to 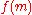 , for a known function
, for a known function  , without necessarily knowing or learning
, without necessarily knowing or learning  .
.
Malleability is often an undesirable property in a general-purpose cryptosystem, since it allows an attacker to modify the contents of a message. For example, suppose that a bank uses a stream cipher to hide its financial information, and a user sends an encrypted message containing, say, "TRANSFER $0000100.00 TO ACCOUNT #199." If an attacker can modify the message on the wire, and can guess the format of the unencrypted message, the attacker could be able to change the amount of the transaction, or the recipient of the funds, e.g. "TRANSFER $0100000.00 TO ACCOUNT #227."
On the other hand, some cryptosystems are malleable by design. In other words, in some circumstances it may be viewed as a feature that anyone can transform an encryption of into a valid encryption of
into a valid encryption of 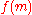 (for some restricted class of functions
(for some restricted class of functions  ) without necessarily learning
) without necessarily learning  . Such schemes are known as homomorphic encryption
. Such schemes are known as homomorphic encryption
schemes.
A cryptosystem may be semantically secure
against chosen plaintext attacks or even non-adaptive chosen ciphertext attacks (CCA1) while still being malleable. However, security against adaptive chosen ciphertext attacks (CCA2) is equivalent to non-malleability.
, the ciphertext is produced by taking the exclusive or of the plaintext and a pseudorandom stream based on a secret key , as
, as 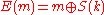 . An adversary can construct an encryption of
. An adversary can construct an encryption of  for any
for any  , as
, as  .
.
In the RSA cryptosystem, a plaintext is encrypted as
is encrypted as  , where
, where 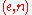 is the public key. Given such a ciphertext, an adversary can construct an encryption of
is the public key. Given such a ciphertext, an adversary can construct an encryption of 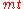 for any
for any  , as
, as  . For this reason, RSA is commonly used together with padding methods such as OAEP
. For this reason, RSA is commonly used together with padding methods such as OAEP
or PKCS1.
In the ElGamal cryptosystem, a plaintext is encrypted as
is encrypted as 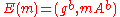 , where
, where 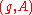 is the public key. Given such a ciphertext
is the public key. Given such a ciphertext 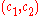 , an adversary can compute
, an adversary can compute 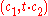 , which is a valid encryption of
, which is a valid encryption of  , for any
, for any  .
.
In contrast, the Cramer-Shoup system (which is based on ElGamal) is not malleable.
In the Paillier
, ElGamal, and RSA cryptosystems, it is also possible to combine several ciphertexts together in a useful way to produce a related ciphertext. In Paillier, given only the public-key and an encryption of and
and 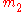 , one can compute a valid encryption of their sum
, one can compute a valid encryption of their sum  . In ElGamal and in RSA, one can combine encryptions of
. In ElGamal and in RSA, one can combine encryptions of  and
and 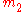 to obtain a valid encryption of their product
to obtain a valid encryption of their product 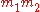 .
.
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. An encryption algorithm is malleable if it is possible for an adversary to transform a ciphertext
Ciphertext
In cryptography, ciphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher...
into another ciphertext which decrypts to a related plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
. That is, given an encryption of a plaintext
 , it is possible to generate another ciphertext which decrypts to
, it is possible to generate another ciphertext which decrypts to 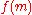 , for a known function
, for a known function  , without necessarily knowing or learning
, without necessarily knowing or learning  .
.Malleability is often an undesirable property in a general-purpose cryptosystem, since it allows an attacker to modify the contents of a message. For example, suppose that a bank uses a stream cipher to hide its financial information, and a user sends an encrypted message containing, say, "TRANSFER $0000100.00 TO ACCOUNT #199." If an attacker can modify the message on the wire, and can guess the format of the unencrypted message, the attacker could be able to change the amount of the transaction, or the recipient of the funds, e.g. "TRANSFER $0100000.00 TO ACCOUNT #227."
On the other hand, some cryptosystems are malleable by design. In other words, in some circumstances it may be viewed as a feature that anyone can transform an encryption of
 into a valid encryption of
into a valid encryption of 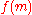 (for some restricted class of functions
(for some restricted class of functions  ) without necessarily learning
) without necessarily learning  . Such schemes are known as homomorphic encryption
. Such schemes are known as homomorphic encryptionHomomorphic encryption
Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
schemes.
A cryptosystem may be semantically secure
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
against chosen plaintext attacks or even non-adaptive chosen ciphertext attacks (CCA1) while still being malleable. However, security against adaptive chosen ciphertext attacks (CCA2) is equivalent to non-malleability.
Example malleable cryptosystems
In a stream cipherStream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
, the ciphertext is produced by taking the exclusive or of the plaintext and a pseudorandom stream based on a secret key
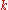 , as
, as 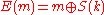 . An adversary can construct an encryption of
. An adversary can construct an encryption of  for any
for any  , as
, as  .
.In the RSA cryptosystem, a plaintext
 is encrypted as
is encrypted as  , where
, where 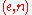 is the public key. Given such a ciphertext, an adversary can construct an encryption of
is the public key. Given such a ciphertext, an adversary can construct an encryption of 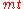 for any
for any  , as
, as  . For this reason, RSA is commonly used together with padding methods such as OAEP
. For this reason, RSA is commonly used together with padding methods such as OAEPOptimal Asymmetric Encryption Padding
In cryptography, Optimal Asymmetric Encryption Padding is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway....
or PKCS1.
In the ElGamal cryptosystem, a plaintext
 is encrypted as
is encrypted as 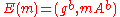 , where
, where 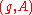 is the public key. Given such a ciphertext
is the public key. Given such a ciphertext 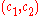 , an adversary can compute
, an adversary can compute 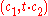 , which is a valid encryption of
, which is a valid encryption of  , for any
, for any  .
.In contrast, the Cramer-Shoup system (which is based on ElGamal) is not malleable.
In the Paillier
Paillier cryptosystem
The Paillier cryptosystem, named after and invented by Pascal Paillier in 1999, is a probabilistic asymmetric algorithm for public key cryptography. The problem of computing n-th residue classes is believed to be computationally difficult...
, ElGamal, and RSA cryptosystems, it is also possible to combine several ciphertexts together in a useful way to produce a related ciphertext. In Paillier, given only the public-key and an encryption of
 and
and 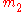 , one can compute a valid encryption of their sum
, one can compute a valid encryption of their sum  . In ElGamal and in RSA, one can combine encryptions of
. In ElGamal and in RSA, one can combine encryptions of  and
and 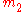 to obtain a valid encryption of their product
to obtain a valid encryption of their product 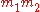 .
.

