
Mathematical constants (sorted by continued fraction representation)
Encyclopedia
This is a list of mathematical constant
s sorted by their representations as continued fraction
s.
Continued fractions with more than 20 known terms have been truncated, with an ellipsis
to show that they continue. Rational numbers have two continued fractions; the version in this list is the shorter one. Decimal representations are rounded
or padded to 10 places if the values are known.
[*]Although some of the symbols in the leftmost column are displayed in black due to math markup peculiarities, all are clickable and link to the respective constant's page.
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s sorted by their representations as continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s.
Continued fractions with more than 20 known terms have been truncated, with an ellipsis
Ellipsis
Ellipsis is a series of marks that usually indicate an intentional omission of a word, sentence or whole section from the original text being quoted. An ellipsis can also be used to indicate an unfinished thought or, at the end of a sentence, a trailing off into silence...
to show that they continue. Rational numbers have two continued fractions; the version in this list is the shorter one. Decimal representations are rounded
Rounding
Rounding a numerical value means replacing it by another value that is approximately equal but has a shorter, simpler, or more explicit representation; for example, replacing $23.4476 with $23.45, or the fraction 312/937 with 1/3, or the expression √2 with 1.414.Rounding is often done on purpose to...
or padded to 10 places if the values are known.
[*]Although some of the symbols in the leftmost column are displayed in black due to math markup peculiarities, all are clickable and link to the respective constant's page.
| Symbol[*] | Member of | decimal | Continued fraction Continued fraction In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on... |
Notes |
|---|---|---|---|---|
 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... |
 Integer The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively... |
0.00000 00000 | [0; ] | |
 |
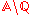 Algebraic number In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental... |
0.61803 39887 | [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …] | First positive irrational number in the list. |
 |
 Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... |
0.64341 05463 | [0; 1, 1, 1, 4, 9, 169, 16641, 639988804, 177227652025317609, 72589906463585427805281295977816196, …] | Continued fraction truncated at 10 terms due to large size. |
 |
 Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... |
0.66016 18158 | [0; 1, 1, 1, 16, 2, 2, 2, 2, 1, 18, 2, 2, 11, 1, 1, 2, 4, 1, 16, 3, …] | Hardy–Littlewood's twin prime constant. Presumed irrational, but not proved. |
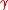 Euler–Mascheroni constant The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter .... |
 |
0.57721 56649 | [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, …] | Presumed irrational, but not proved. |
 |
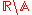 Transcendental number In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e... |
0.56714 32904 | [0; 1, 1, 3, 4, 2, 10, 4, 1, 1, 1, 1, 2, 7, 306, 1, 5, 1, 2, 1, 5, …] | |
 |
 |
0.70258 | [0; 1, 2, 2, 1, 3, 5, 1, 2, 6, 1, 1, 5, …] | Value only known to 5 decimal places. |
 |
 |
0.76422 36535 | [0; 1, 3, 4, 6, 1, 15, 1, 2, 2, 3, 1, 23, 3, 1, 1, 3, 1, 1, 7, 2, …] | May have been proven irrational. |
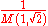 Gauss's constant In mathematics, Gauss's constant, denoted by G, is defined as the reciprocal of the arithmetic-geometric mean of 1 and the square root of 2:The constant is named after Carl Friedrich Gauss, who on May 30, 1799 discovered thatso that... |
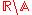 |
0.83462 68417 | [0; 1, 5, 21, 3, 4, 14, 1, 1, 1, 1, 1, 3, 1, 15, 1, 3, 8, 36, 1, 2, …] | Gauss's constant |
 |
 |
0.87058 83800 | [0; 1, 6, 1, 2, 1, 2, 956, 8, 1, 1, 1, 23, …] | Brun's prime quadruplet constant. Estimated value; 99% confidence interval ± 0.00000 00005. |
 Champernowne constant In mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G... |
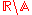 |
0.86224 01259 | [0; 1, 6, 3, 1, 6, 5, 3, 3, 1, 6, 4, 1, 3, 298, 1, 6, 1, 1, 3, 285, …] | Base 2 Champernowne constant. The binary expansion is  |
 |
 |
0.91596 55942 | [0; 1, 10, 1, 8, 1, 88, 4, 1, 1, 7, 22, 1, 2, 3, 26, 1, 11, 1, 10, 1, …] | Presumed irrational, but not proved. |
 |
 Rational number In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number... |
0.50000 00000 | [0; 2] | |
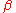 Bernstein's constant Bernstein's constant, usually denoted by the Greek letter β , is a mathematical constant named after Sergei Natanovich Bernstein and is approximately equal to 0.2801694990.- Definition :... |
 |
0.28016 94990 | [0; 3, 1, 1, 3, 9, 6, 3, 1, 3, 13, 1, 16, 3, 3, 4, …] | Presumed irrational, but not proved. |
 |
 |
0.26149 72128 | [0; 3, 1, 4, 1, 2, 5, 2, 1, 1, 1, 1, 13, 4, 2, 4, 2, 1, 33, 296, 2, …] | Presumed irrational, but not proved. |
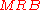 MRB constant The MRB constant, named after Marvin Ray Burns, is a mathematical constant for which no closed-form expression is known. It is not known whether the MRB constant is algebraic, transcendental, or even irrational.... |
 |
0.18785 96424 | [0; 5, 3, 10, 1, 1, 4, 1, 1, 1, 1, 9, 1, 1, 12, 2, 17, 2, 2, 1, 1, …] | |
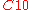 Champernowne constant In mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G... |
 |
0.12345 67891 | [0; 8, 9, 1, 149083, 1, 1, 1, 4, 1, 1, 1, 3, 4, 1, 1, 1, 15,  , 6, 1, …] , 6, 1, …] |
Base 10 Champernowne constant. Champernowne constants in any base exhibit sporadic large numbers; the 40th term in 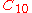 has 2504 digits. has 2504 digits. |
 |
 Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... |
1.00000 00000 | [1; ] | |
 Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... |
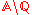 |
1.61803 39887 | [1; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …] | |
 |
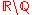 Irrational number In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number.... |
1.60669 51524 | [1; 1, 1, 1, 1, 5, 2, 1, 2, 29, 4, 1, 2, 2, 2, 2, 6, 1, 7, 1, 6, …] | Not known whether algebraic or transcendental. |
 |
 |
1.90216 05823 | [1; 1, 9, 4, 1, 1, 8, 3, 4, 7, 1, 3, 3, 1, 2, 1, 1, 12, 4, 2, 1, …] | Brun's twin prime constant. Estimated value; best bounds  . . |
 Backhouse's constant Backhouse's constant is a mathematical constant founded by N. Backhouse and is approximately 1.456 074 948.It is defined by using the power series such that the coefficients of successive terms are the prime numbers:and whereThen:... |
 |
1.45607 49485 | [1; 2, 5, 5, 4, 1, 1, 18, 1, 1, 1, 1, 1, 2, 13, 3, 1, 2, 4, 16, 4,, …] | |
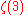 Apéry's constant In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics... |
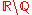 |
1.20205 69032 | [1; 4, 1, 18, 1, 1, 1, 4, 1, 9, 9, 2, 1, 1, 1, 2, 7, 1, 1, 7, 11, …] | |
 |
 |
1.13198 82488 | [1; 7, 1, 1, 2, 1, 3, 2, 1, 2, 1, 17, 1, 1, 2, 1, 2, 4, 1, 2, …] | Viswanath's constant. Apparently, Eric Weisstein calculated this constant to be approximately 1.13215 06911 with Mathematica. |
 Square root of 2 The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the... |
 |
1.41421 35624 | [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, …] | |
 Ramanujan-Soldner constant In mathematics, the Ramanujan–Soldner constant is a mathematical constant defined as the unique positive zero of the logarithmic integral function... |
 |
1.45136 92349 | [1; 2, 4, 1, 1, 1, 3, 1, 1, 1, 2, 47, 2, 4, 1, 12, 1, 1, 2, 2, 1, …] | Presumed irrational, but not proved. |
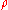 Plastic number In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, .... |
 |
1.32471 95724 | [1; 3, 12, 1, 1, 3, 2, 3, 2, 4, 2, 141, 80, 2, 5, 1, 2, 8, 2, 1, 1, …] | |
 |
 |
2.00000 00000 | [2; ] | |
 |
 |
2.66514 41426 | [2; 1, 1, 1, 72, 3, 4, 1, 3, 2, 1, 1, 1, 14, 1, 2, 1, 1, 3, 1, 3, …] | |
 Feigenbaum constants The Feigenbaum constants are two mathematical constants named after the mathematician Mitchell Feigenbaum. Both express ratios in a bifurcation diagram.The first Feigenbaum constant ,... |
 |
2.50290 78751 | [2; 1, 1, 85, 2, 8, 1, 10, 16, 3, 8, 9, 2, 1, 40, 1, 2, 3, 2, 2, 1, …] | |
 E (mathematical constant) The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base... |
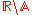 |
2.71828 18285 | [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, …] | |
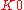 |
 |
2.68545 20011 | [2; 1, 2, 5, 1, 1, 2, 1, 1, 3, 10, 2, 1, 3, 2, 24, 1, 3, 2, 3, 1, …] | |
 |
 |
2.80777 02420 | [2; 1, 4, 4, 1, 18, 5, 1, 3, 4, 1, 5, 3, 6, 1, 1, 1, 5, 1, 1, 1, …] | |
 Universal parabolic constant The universal parabolic constant is a mathematical constant.It is defined as the ratio, for any parabola, of the arc length of the parabolic segment formed by the latus rectum to the focal parameter... |
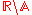 |
2.29558 71494 | [2; 3, 2, 1, 1, 1, 1, 3, 3, 1, 1, 4, 2, 3, 2, 7, 1, 6, 1, 8, 7, …] | |
 |
 |
3.00000 00000 | [3; ] | |
 Pi ' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants... |
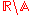 |
3.14159 26536 | [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, …] | |
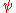 |
 |
3.35988 56662 | [3; 2, 1, 3, 1, 1, 13, 2, 3, 3, 2, 1, 1, 6, 3, 2, 4, 362, 2, 4, 8, …] | |
 |
 |
4.00000 00000 | [4; ] | |
 Feigenbaum constants The Feigenbaum constants are two mathematical constants named after the mathematician Mitchell Feigenbaum. Both express ratios in a bifurcation diagram.The first Feigenbaum constant ,... |
 |
4.66920 16091 | [4; 1, 2, 43, 2, 163, 2, 3, 1, 1, 2, 5, 1, 2, 3, 80, 2, 5, 2, 1, 1, …] | |
 Gelfond's constant In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that... |
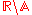 |
23.14069 26328 | [23; 7, 9, 3, 1, 1, 591, 2, 9, 1, 2, 34, 1, 16, 1, 30, 1, 1, 4, 1, 2, …] | Gelfond's constant. Can also be expressed as 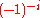 ; from this form, it is transcendental due to the Gelfond–Schneider theorem ; from this form, it is transcendental due to the Gelfond–Schneider theoremGelfond–Schneider theorem In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider... . |

