
Maximal semilattice quotient
Encyclopedia
In abstract algebra
, a branch of mathematics
, a maximal semilattice quotient is a commutative monoid derived from another commutative monoid by making certain elements equivalent
to each other.
Every commutative monoid
can be endowed with its algebraic preorder
ing ≤ . By definition, x≤ y holds, if there exists z such that x+z=y. Further, for x, y in M, let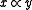 hold, if there exists a positive integer n such that x≤ ny, and let
hold, if there exists a positive integer n such that x≤ ny, and let 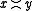 hold, if
hold, if 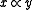 and
and 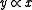 . The binary relation
. The binary relation
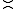 is a monoid congruence
is a monoid congruence
of M, and the quotient monoid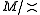 is the maximal semilattice quotient of M.
is the maximal semilattice quotient of M.
This terminology can be explained by the fact that the canonical projection p from M onto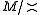 is universal among all monoid homomorphisms from M to a (∨,0)-semilattice
is universal among all monoid homomorphisms from M to a (∨,0)-semilattice
, that is, for any (∨,0)-semilattice S and any monoid homomorphism f: M→ S, there exists a unique (∨,0)-homomorphism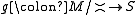 such that f=gp.
such that f=gp.
If M is a refinement monoid
, then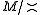 is a distributive semilattice
is a distributive semilattice
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a maximal semilattice quotient is a commutative monoid derived from another commutative monoid by making certain elements equivalent
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
to each other.
Every commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
can be endowed with its algebraic preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
ing ≤ . By definition, x≤ y holds, if there exists z such that x+z=y. Further, for x, y in M, let
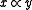 hold, if there exists a positive integer n such that x≤ ny, and let
hold, if there exists a positive integer n such that x≤ ny, and let 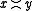 hold, if
hold, if 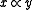 and
and 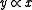 . The binary relation
. The binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
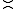 is a monoid congruence
is a monoid congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
of M, and the quotient monoid
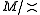 is the maximal semilattice quotient of M.
is the maximal semilattice quotient of M.This terminology can be explained by the fact that the canonical projection p from M onto
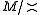 is universal among all monoid homomorphisms from M to a (∨,0)-semilattice
is universal among all monoid homomorphisms from M to a (∨,0)-semilatticeSemilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
, that is, for any (∨,0)-semilattice S and any monoid homomorphism f: M→ S, there exists a unique (∨,0)-homomorphism
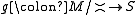 such that f=gp.
such that f=gp.If M is a refinement monoid
Refinement monoid
In mathematics, a refinement monoid is a commutative monoid M such that for any elements a0, a1, b0, b1 of M such that a0+a1=b0+b1, there are elements c00, c01, c10, c11 of M such that a0=c00+c01, a1=c10+c11, b0=c00+c10, and b1=c01+c11.A commutative monoid M is conical, if x+y=0 implies that x=y=0,...
, then
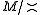 is a distributive semilattice
is a distributive semilatticeDistributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
.

