
Maximum Likelihood Sequence Estimation
Encyclopedia
Maximum likelihood sequence estimation (MLSE) is a mathematical algorithm to extract useful data out of a noisy data stream.
The receiver emulates the distorted channel. All possible transmitted data streams are fed into this distorted channel model. The receiver compares the time response with the actual received signal and determines the most likely signal.
In cases that are most computationally straightforward, root mean square deviation
can be used as the decision criterion for the lowest error probability.
s of this transformation are assumed known. The problem to be solved is to use the observations {r(t)} to create a good estimate of {x(t)}.
Maximum likelihood sequence estimation is formally the application of maximum likelihood
to this problem. That is, the estimate of {x(t)} is defined to be sequence of values which maximize the functional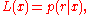
where p(r|x) denotes the conditional joint probability density function of the observed series {r(t)} given that the underlying series has the values {x(t)}.
In contrast, the related method of maximum a posteriori estimation is formally the application of the Maximum a posteriori
(MAP) estimation approach. This is more complex than maximum likelihood sequence estimation and requires a known distribution (in Bayesian terms
, a prior distribution) for the underlying signal. In this case the estimate of {x(t)} is defined to be sequence of values which maximize the functional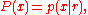
where p(x|r) denotes the conditional joint probability density function of the underlying series {x(t)} given that the observed series has taken the values {r(t)}. Bayes' theorem
implies that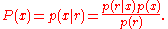
In cases where the contribution of random noise is additive and has a multivariate normal distribution, the problem of maximum likelihood sequence estimation can be reduced to that of a least squares
minimization.
Theory
For an optimized detector for digital signals the priority is not to reconstruct the transmitter signal, but it should do a best estimation of the transmitted data with the least possible number of errors.The receiver emulates the distorted channel. All possible transmitted data streams are fed into this distorted channel model. The receiver compares the time response with the actual received signal and determines the most likely signal.
In cases that are most computationally straightforward, root mean square deviation
Root mean square deviation
The root-mean-square deviation is the measure of the average distance between the atoms of superimposed proteins...
can be used as the decision criterion for the lowest error probability.
Background
Suppose that there is an underlying signal {x(t)}, of which an observed signal {r(t)} is available. The observed signal r is related to x via a transformation that may be nonlinear and may involve attenuation, and would usually involve the incorporation of random noise. The statistical parameterStatistical parameter
A statistical parameter is a parameter that indexes a family of probability distributions. It can be regarded as a numerical characteristic of a population or a model....
s of this transformation are assumed known. The problem to be solved is to use the observations {r(t)} to create a good estimate of {x(t)}.
Maximum likelihood sequence estimation is formally the application of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
to this problem. That is, the estimate of {x(t)} is defined to be sequence of values which maximize the functional
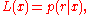
where p(r|x) denotes the conditional joint probability density function of the observed series {r(t)} given that the underlying series has the values {x(t)}.
In contrast, the related method of maximum a posteriori estimation is formally the application of the Maximum a posteriori
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) estimation approach. This is more complex than maximum likelihood sequence estimation and requires a known distribution (in Bayesian terms
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, a prior distribution) for the underlying signal. In this case the estimate of {x(t)} is defined to be sequence of values which maximize the functional
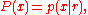
where p(x|r) denotes the conditional joint probability density function of the underlying series {x(t)} given that the observed series has taken the values {r(t)}. Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
implies that
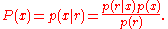
In cases where the contribution of random noise is additive and has a multivariate normal distribution, the problem of maximum likelihood sequence estimation can be reduced to that of a least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
minimization.
Further reading
- Crivelli, D. E.; Carrer, H. S., Hueda, M. R. (2005) "Performance evaluation of maximum likelihood sequence estimation receivers in lightwave systems with optical amplifiers", Latin American Applied Research, 35 (2), 95–98.
- Katz, G., Sadot, D., Mahlab, U., and Levy, A.(2008) "Channel estimators for maximum-likelihood sequence estimation in direct-detection optical communications", Optical Engineering 47 (4), 045003.

