Maxwell material
Encyclopedia
A Maxwell material is a viscoelastic material having the properties both of elasticity
and viscosity
. It is named for James Clerk Maxwell
who proposed the model in 1867. It is also known as a Maxwell fluid.
and the total strain, 
can be defined as follows:
where the subscript D indicates the stress/strain in the damper and the subscript S indicates the stress/strain in the spring. Taking the derivative of strain with respect to time, we obtain:
where E is the elastic modulus and η is the material coefficient of viscosity. This model describes the damper as a Newtonian fluid
and models the spring with Hooke's law
.
If we connect these two elements in parallel, we get a model of Kelvin-Voigt material
.
In a Maxwell material, stress
σ, strain
ε and their rates of change with respect to time t are governed by equations of the form:
or, in dot notation:
The equation can be applied either to the shear stress
or to the uniform tension in a material. In the former case, the viscosity corresponds to that for a Newtonian fluid
. In the latter case, it has a slightly different meaning relating stress and rate of strain.
The model is usually applied to the case of small deformations. For the large deformations we should include some geometrical non-linearity. For the simplest way of generalizing the Maxwell model, refer to the Upper Convected Maxwell
Model.
of
, then the stress decays with a characteristic time of 
.
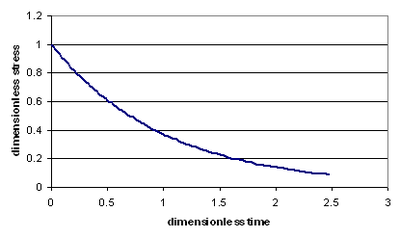
The picture shows dependence of dimensionless stress
upon dimensionless time
:
If we free the material at time 
, then the elastic element will spring back by the value of
Since the viscous element would not return to its original length, the irreversible component of deformation can be simplified to the expression below:
, then the elastic element would suddenly deform and the viscous element would deform with a constant rate:
If at some time
we would release the material, then the deformation of the elastic element would be the spring-back deformation and the deformation of the viscous element would not change:
The Maxwell Model does not exhibit creep
since it models strain as linear function of time.
If a small stress is applied for a sufficiently long time, then the irreversible stresses become large. Thus, Maxwell material is a type of liquid
.
of a Maxwell material would be:
Thus, the components of the dynamic modulus are :
and
The picture shows relaxational spectrum for Maxwell material. The relaxation time constant is 
.
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. It is named for James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
who proposed the model in 1867. It is also known as a Maxwell fluid.
Definition
The Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series, as shown in the diagram. In this configuration, under an applied axial stress, the total stress, and the total strain, can be defined as follows:where the subscript D indicates the stress/strain in the damper and the subscript S indicates the stress/strain in the spring. Taking the derivative of strain with respect to time, we obtain:
where E is the elastic modulus and η is the material coefficient of viscosity. This model describes the damper as a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
and models the spring with Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
.
If we connect these two elements in parallel, we get a model of Kelvin-Voigt material
Kelvin-Voigt material
A Kelvin–Voigt material, also called a Voigt material, is a viscoelastic material having the properties both of elasticity and viscosity. It is named after the British physicist and engineer William Thomson, 1st Baron Kelvin and after German physicist Woldemar Voigt.- Definition :The Kelvin–Voigt...
.
In a Maxwell material, stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
σ, strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
ε and their rates of change with respect to time t are governed by equations of the form:
or, in dot notation:
The equation can be applied either to the shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
or to the uniform tension in a material. In the former case, the viscosity corresponds to that for a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
. In the latter case, it has a slightly different meaning relating stress and rate of strain.
The model is usually applied to the case of small deformations. For the large deformations we should include some geometrical non-linearity. For the simplest way of generalizing the Maxwell model, refer to the Upper Convected Maxwell
Upper Convected Maxwell
The Upper Convected Maxwell model is a generalisation of the Maxwell material for the case of large deformations using the Upper convected time derivative. The model was proposed by James G...
Model.
Effect of a sudden deformation
If a Maxwell material is suddenly deformed and held to a strainStrain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
of
, then the stress decays with a characteristic time of .The picture shows dependence of dimensionless stress
upon dimensionless time
:, then the elastic element will spring back by the value ofSince the viscous element would not return to its original length, the irreversible component of deformation can be simplified to the expression below:
Effect of a sudden stress
If a Maxwell material is suddenly subjected to a stress, then the elastic element would suddenly deform and the viscous element would deform with a constant rate:If at some time
we would release the material, then the deformation of the elastic element would be the spring-back deformation and the deformation of the viscous element would not change:The Maxwell Model does not exhibit creep
Creep (deformation)
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
since it models strain as linear function of time.
If a small stress is applied for a sufficiently long time, then the irreversible stresses become large. Thus, Maxwell material is a type of liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
.
Dynamic modulus
The complex dynamic modulusDynamic modulus
Dynamic modulus is the ratio of stress to strain under vibratory conditions...
of a Maxwell material would be:
Thus, the components of the dynamic modulus are :
and
.
| Blue curve | dimensionless elastic modulus  |
| Pink curve | dimensionless modulus of losses  |
| Yellow curve | dimensionless apparent viscosity  |
| X-axis | dimensionless frequency  . |
See also
- Generalized Maxwell material
- Kelvin-Voigt materialKelvin-Voigt materialA Kelvin–Voigt material, also called a Voigt material, is a viscoelastic material having the properties both of elasticity and viscosity. It is named after the British physicist and engineer William Thomson, 1st Baron Kelvin and after German physicist Woldemar Voigt.- Definition :The Kelvin–Voigt...
- Oldroyd material
- Standard Linear Solid Material
- Upper Convected Maxwell model