Upper Convected Maxwell
Encyclopedia
The Upper Convected Maxwell model (or UCM model) is a generalisation of the Maxwell material
for the case of large deformations using the Upper convected time derivative. The model was proposed by James G. Oldroyd
.
The model can be written as: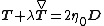
where:
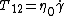
and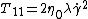
where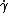
is the shear rate.
Thus, the Upper Convected Maxwell model predicts for the simple shear that shear stress
to be proportional to the shear rate and the first difference of normal stresses (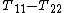
) is proportional to the square of the shear rate, the second difference of normal stresses (
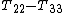) is always zero. In other words, UCM predicts appearance of the first difference of normal stresses but does not predict non-Newtonian behavior
of the shear viscosity nor the second difference of the normal stresses.
Usually quadratic behavior of the first difference of normal stresses and no second difference of the normal stresses is a realistic behavior of polymer melts at moderated shear rates, but constant viscosity is unrealistic and limits usability of the model.
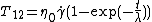
and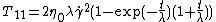
The equations above describe stresses gradually risen from zero the steady-state values.
The equation is only applicable, when the velocity profile in the shear flow is fully developed. Then the shear rate is constant over the channel height. If the start-up form a zero velocity distribution has to be calculated, the full set of PDEs has to be solved.
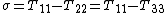calculated by the following equation:
where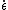
is the elongation rate.
The equation predicts the elongation viscosity approaching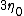
(the same as for the Newtonian fluid
s) for the case of low elongation rate (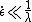
) with fast deformation thickening with the steady state viscosity approaching infinity at some elongational rate (
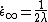) and at some compression rate (
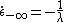). This behavior seems to be realistic.
.
Maxwell material
A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.- Definition :...
for the case of large deformations using the Upper convected time derivative. The model was proposed by James G. Oldroyd
James G. Oldroyd
James Gardner Oldroyd was British mathematician and noted rheologist. He formulated the Oldroyd-B model to describe the viscoelastic behaviour of non-Newtonian fluids.-Life:...
.
The model can be written as:
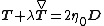
where:
-
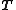is the stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
; -
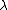is the relaxation time; -
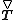is the Upper convected time derivative of stress tensor: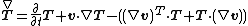
is the fluid velocity
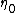is material viscosityViscosityViscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
at steady simple shearSimple shearIn fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
;
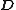is the tensor of the deformation rate.
Case of the Steady Shear
For this case only two components of the shear stress became non-zero: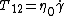and
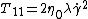
where
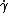is the shear rate.Thus, the Upper Convected Maxwell model predicts for the simple shear that shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
to be proportional to the shear rate and the first difference of normal stresses (
) is proportional to the square of the shear rate, the second difference of normal stresses () is always zero. In other words, UCM predicts appearance of the first difference of normal stresses but does not predict non-Newtonian behaviorNon-Newtonian fluid
A non-Newtonian fluid is a fluid whose flow properties differ in any way from those of Newtonian fluids. Most commonly the viscosity of non-Newtonian fluids is not independent of shear rate or shear rate history...
of the shear viscosity nor the second difference of the normal stresses.
Usually quadratic behavior of the first difference of normal stresses and no second difference of the normal stresses is a realistic behavior of polymer melts at moderated shear rates, but constant viscosity is unrealistic and limits usability of the model.
Case of start-up of Steady Shear
For this case only two components of the shear stress became non-zero:and
The equations above describe stresses gradually risen from zero the steady-state values.
The equation is only applicable, when the velocity profile in the shear flow is fully developed. Then the shear rate is constant over the channel height. If the start-up form a zero velocity distribution has to be calculated, the full set of PDEs has to be solved.
Case of the Steady State Uniaxial Extension or Uniaxial Compression
For this case UCM predicts the normal stresses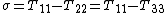 calculated by the following equation:
where
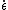is the elongation rate.The equation predicts the elongation viscosity approaching
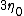(the same as for the Newtonian fluidNewtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
s) for the case of low elongation rate (
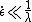) with fast deformation thickening with the steady state viscosity approaching infinity at some elongational rate (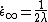) and at some compression rate (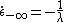). This behavior seems to be realistic.Case of small deformation
For the case of small deformation the nonlinearities introduced by the Upper Convected Derivative disappear and the model became an ordinary model of Maxwell materialMaxwell material
A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.- Definition :...
.