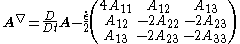Upper convected time derivative
Encyclopedia
In continuum mechanics
, including fluid dynamics
, upper convected time derivative or Oldroyd derivative is the rate of change
of some tensor
property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid.
The operator is specified by the following formula:
where:
The formula can be rewritten as:
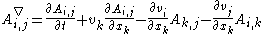
By definition the upper convected time derivative of the Finger tensor is always zero.
The upper convected derivatives is widely use in polymer
rheology
for the description of behavior of a visco-elastic fluid under large deformations.
Simple shear
For the case of simple shear
: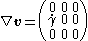
Thus,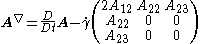
The gradients of velocity are: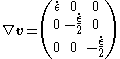
Thus,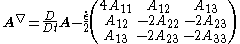
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, including fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, upper convected time derivative or Oldroyd derivative is the rate of change
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of some tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid.
The operator is specified by the following formula:

where:
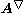 is the Upper convected time derivative of a tensor fieldField (physics)In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
is the Upper convected time derivative of a tensor fieldField (physics)In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
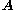
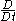 is the Substantive derivative
is the Substantive derivative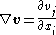 is the tensor of velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
is the tensor of velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s for the fluid.
The formula can be rewritten as:
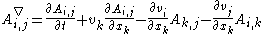
By definition the upper convected time derivative of the Finger tensor is always zero.
The upper convected derivatives is widely use in polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
rheology
Rheology
Rheology is the study of the flow of matter, primarily in the liquid state, but also as 'soft solids' or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force....
for the description of behavior of a visco-elastic fluid under large deformations.
Simple shearSimple shearIn fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
For the case of simple shearSimple shear
In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
:
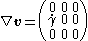
Thus,
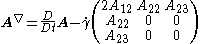
Uniaxial extension of uncompressible fluid
In this case a material is stretched in the direction X and compresses in the direction s Y and Z, so to keep volume constant.The gradients of velocity are:
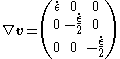
Thus,