
Mean of circular quantities
Encyclopedia
In mathematics
, a mean of circular quantities is a mean
which is suited for quantities like angle
s, daytime
s, and fractional part
s of real number
s. This is necessary since most of the usual means fail on circular quantities. For example, the arithmetic mean of 0° and 360° is 180°, although 0° would be clearly the better choice.
This is one of the simplest examples of statistics of non-Euclidean spaces.
of the angles:
Convert all angles to corresponding points on the unit circle
, e.g., to
to 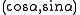 . That is convert polar coordinates to Cartesian coordinates. Then compute the arithmetic mean
. That is convert polar coordinates to Cartesian coordinates. Then compute the arithmetic mean
of these points. The resulting point will lie on the unit disk. Convert that point back to polar coordinates. The angle is a reasonable mean of the input angles. The resulting radius will be 1 if all angles are equal. If the angles are uniformly distributed on the circle, then the resulting radius will be 0, and there is no circular mean. In other words, the radius measures the concentration of the angles.
Given the angles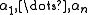 the mean is computed by
the mean is computed by

using the atan2
variant of the arctangent function, or
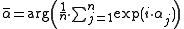
using complex number
s.

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a mean of circular quantities is a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
which is suited for quantities like angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s, daytime
DAYTIME
The Daytime Protocol is a service in the Internet Protocol Suite, defined in 1983 in RFC 867. It is intended for testing and measurement purposes in computer networks....
s, and fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
s of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. This is necessary since most of the usual means fail on circular quantities. For example, the arithmetic mean of 0° and 360° is 180°, although 0° would be clearly the better choice.
This is one of the simplest examples of statistics of non-Euclidean spaces.
Mean of angles
Since the arithmetic mean is not effective for angles, the following method can be used to obtain both a mean value and measure for the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the angles:
Convert all angles to corresponding points on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, e.g.,
 to
to 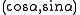 . That is convert polar coordinates to Cartesian coordinates. Then compute the arithmetic mean
. That is convert polar coordinates to Cartesian coordinates. Then compute the arithmetic meanArithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of these points. The resulting point will lie on the unit disk. Convert that point back to polar coordinates. The angle is a reasonable mean of the input angles. The resulting radius will be 1 if all angles are equal. If the angles are uniformly distributed on the circle, then the resulting radius will be 0, and there is no circular mean. In other words, the radius measures the concentration of the angles.
Given the angles
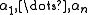 the mean is computed by
the mean is computed by
using the atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
variant of the arctangent function, or
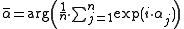
using complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Properties
The mean
- maximizes the likelihoodLikelihoodLikelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
of the mean parameter of the von Mises distribution and - minimizes the sum of a certain distance on the circle, more precisely
-
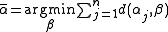 , where
, where 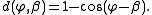
- The distance
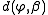 is equal to half the squared Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
is equal to half the squared Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between the two points on the unit circle associated with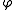 and
and 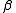 .
.

