
Mediation (Statistics)
Encyclopedia
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a mediation model is one that seeks to identify and explicate the mechanism that underlies an observed relationship between an independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
and a dependent variable via the inclusion of a third explanatory variable, known as a mediator variable. Rather than hypothesizing a direct causal relationship between the independent variable and the dependent variable, a mediational model hypothesizes that the independent variable causes the mediator variable, which in turn causes the dependent variable. The mediator variable, then, serves to clarify the nature of the relationship between the independent and dependent variables. While the concept of mediation as defined within psychology is theoretically appealing, the methods used to study mediation empirically have been challenged by statisticians and epidemiologists and interpreted formally.
Direct versus indirect effects
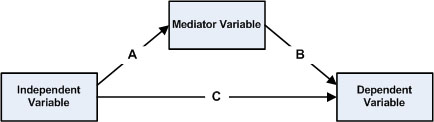
In the diagram shown above, assuming linear relationships,the indirect effect is the product of paths coefficients A
and B, while the direct effect is the coefficient C.
The total effect measures the
extent to which the dependent variable changes when the
independent variable increases by one unit.
In contrast, the indirect effect
(sometimes referred to as mediated effect) measures the
extent to which the dependent variable changes when the
independent variable is held fixed and the mediator variable
changes to the level it would have attained had the
independent variable increased by one unit.
In linear systems, the total effect is equal to the
sum of the direct and indirect effects (C + AB in the model
above). In nonlinear models, the total
effect is not generally equal to the sum of the direct
and indirect effects, but to a modified
combination of the two.
Complete versus partial mediation
When the measured effect between the independent variable andthe dependent variable is zero upon fixing the mediator
variable, the mediation effect is said to be complete
(C = 0 in the diagram above.)
If, however, the measured effect changes upon fixing
the mediator but remains significantly different from zero,
the mediation effect is said to be partial. In all cases,
the operation of "fixing a variable" must be distinguished
from that of "controlling for a variable," which has been
inappropriately used in the literature. The
former stands for physically fixing, while the latter
stands for conditioning on, adjusting for, or adding to
the regression model. The two notions coincide only
when all error terms (not shown in the diagram) are
statistically uncorrelated. When errors are correlated,
adjustments must be made to neutralize those
correlations before embarking on mediation analysis (see Bayesian Networks).
In order for either partial or complete mediation to be
established, the reduction in variance explained by the
independent variable must be significant as determined by
one of several tests, such as the Sobel test (1982). The
effect of an independent variable on the dependent variable
can become nonsignificant when the mediator is introduced
simply because a trivial amount of variance is explained
(i.e., not true mediation). Thus, it is imperative to show a
significant reduction in variance explained by the
independent variable before asserting either partial or
complete mediation. Hayes (2009) shows that it is
possible to have statistically significant indirect effects
in the absence of a total effect. This can be explained
by the presence of several mediating paths that cancel
each other out, and become noticeable when one
of the cancelling mediator is controlled for.
This implies that the terms 'complete' and 'partial' mediation
should always be interpreted relative to the set of variables
that are present in the model.
Suppression
Suppression is defined as "a variable which increases thepredictive validity of another variable (or set of
variables) by its inclusion into a regression equation".
For instance, if you are set to examine the effect of a
treatment (e.g. medication) on an outcome (e.g. healing from
a disease), a suppression would mean that instead of the
drop that you would see from the direct effect of the
treatment on the outcome when the mediator is included,
the opposite happens. The inclusion of the suppressor variable in the equation increases, rather than decreases
the relation between the treatment and outcome.
This, too, can be explained by cancelation; disabling
one mediating path may disturb the balance between otherwise
cancelling paths.
Pearl (2000, page 139) has argued that "suppression"
may emanate from confusing causal and
associational relationships, as in Simpson's paradox
Simpson's paradox
In probability and statistics, Simpson's paradox is a paradox in which a correlation present in different groups is reversed when the groups are combined. This result is often encountered in social-science and medical-science statistics, and it occurs when frequencydata are hastily given causal...
.
Moderated mediation
Mediation and moderationModeration (statistics)
In statistics, moderation occurs when the relationship between two variables depends on a third variable. The third variable is referred to as the moderator variable or simply the moderator...
can co-occur in statistical models. It is possible to mediate moderation and moderate mediation.
Moderated mediation is when the effect of the treatment effect A on the mediator B, and/or when the partial effect of B on C, depends on levels of another variable (D). This definition has been outlined by Muller, Judd, and Yzerbyt (2005) and Preacher, Rucker, and Hayes (2007).
Mediated moderation
Mediated moderation is a variant of both moderation and mediation. This is where there is initially overall moderation and the direct effect of the moderator variable on the outcome, is mediated either at the A ← B path or at the B → C. The main difference between mediated moderation and moderated mediation is that for the former there is initial moderation and this effect is mediated and for the latter there is no moderation but the effect of either the treatment (A) on the mediator (B) is moderated or the effect of the mediator (B) on the outcome (C) is moderated.Mediator variable
A mediator variable (or mediating variable, or intervening variable) in statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
is a variable that describes how rather than when effects will occur by accounting for the relationship between the independent and dependent variables. A mediating relationship is one in which the path relating A to C is mediated by a third variable (B).
For example, a mediating variable explains the actual relationship between the following variables. Most people will agree that older drivers (up to a certain point), are better drivers. Thus:
- aging
 better driving
better driving
But what is missing from this relationship is a mediating variable that is actually causing the improvement in driving: experience. The mediated relationship would look like the following:
- aging
 increased experience driving a car
increased experience driving a car  better driving
better driving
Mediating variables are often contrasted with moderating variables, which pinpoint the conditions under which an independent variable exerts its effects on a dependent variable. A moderating relationship can be thought of as an interaction. It occurs when the relationship between variables A and B depends on the level of C.
Significance of mediation
BootstrappingBootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
http://www.comm.ohio-state.edu/ahayes/sobel.htm http://www.psych.ku.edu/preacher/sobel/sobel.htmhttp://www.comm.ohio-state.edu/ahayes/SPSS%20programs/indirect.htm is becoming the most popular method of testing mediation because it does not require the normality assumption to be met, and because it can be effectively utilized with smaller sample sizes (N<25). However, mediation continues to be most frequently determined using the (1) the logic of Baron and Kenny http://davidakenny.net/cm/mediate.htm or (2) the Sobel test. However, this is changing, and it is becoming increasingly more difficult to publish tests of mediation based purely on the Baron and Kenny method or tests that make distributional assumptions such as the Sobel test. See Hayes (2009) for a discussion.
The Mediation Formula
Baron and Kenny's method of evaluating the degree to whichan effect is mediated by a given path is applicable
in linear systems only. In nonlinear models, especially
those involving categorical variables and strong interactions,
direct and indirect effects cannot be defined in terms
of adding the putative mediator variable to a regression model.
Instead, the following counterfactual
definitions must be invoked :
The direct effect DE measures the expected change
in the dependent variable (Y) when the
independent variable (X) is increased by one unit,
say from x to x+1, while the mediator variable (M)
is held fixed at the level it would have attained
before the change.
The indirect effect IE measures the expected
change in the dependent variable (Y) when the
independent variable (X) is held fixed, and the
mediator variable (M) changes to the level it would have
attained had the independent variable increased by one unit,
say from x to x+1.
For the case of error independence (or no confoundedness),
Pearl derived closed-form expressions for both
DE and IE, called the Mediation Formulas:

where m ranges over the values that the mediator variable
can take.
DE gives the effect remaining after suppressing the M-mediated
path, while IE gives the effect remaining after suppressing
the direct path from X to Y.
If TE is the total effect, then 1-DE/TE measures the
fraction of response owed to mediation, while IE/TE measures
the fraction explained by mediation. When the output (Y) is binary,
1-DE/TE measures the percentage of responding units
for which mediation was necessary, while IE/TE measures
the percentage for which mediation was sufficient.
The Mediation Formulas are applicable to all distributions,
and to all types of variables, and they enable analysts to
estimate direct and indirect effects efficiently, using
both parametric and nonparametric regression.
Due to non-linearities, the total effect may be
non-zero even in the absence of direct and indirect effects.
This would occur, for example, when Y requires the
presence of both M=1 and X=1, and M=X; neither the direct
nor indirect path alone can trigger a response while
the combined paths can.

