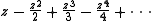Mercator series
Encyclopedia
In mathematics
, the Mercator series or Newton–Mercator series is the Taylor series
for the natural logarithm
:
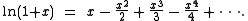
In summation notation,
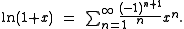
The series converges to the natural logarithm (shifted by 1) whenever −1 < x ≤ 1.
, Isaac Newton
and Gregory Saint-Vincent. It was first published by Mercator, in his 1668 treatise Logarithmo-technica.
, by inductively computing the nth derivative of ln x at x = 1, starting with
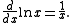
Alternatively, one can start with the finite geometric series (t ≠ −1)
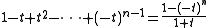
which gives

It follows that

and by termwise integration,
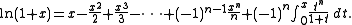
If −1 < x ≤ 1, the remainder term tends to 0 as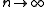 .
.
This expression may be integrated iteratively k more times to yield
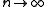
where
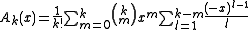
and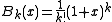
are polynomials in x.
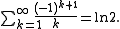
power series
is the Taylor series
for ln(1 + z), where ln denotes the principal branch
of the complex logarithm
. This series converges within the open unit disk |z| < 1 and on the circle |z| = 1 except at z = -1 (due to Abel's test), and the convergence is uniform on each closed disk of radius strictly less than 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Mercator series or Newton–Mercator series is the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
:
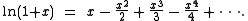
In summation notation,
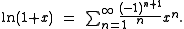
The series converges to the natural logarithm (shifted by 1) whenever −1 < x ≤ 1.
History
The series was discovered independently by Nicholas MercatorNicholas Mercator
Nicholas Mercator , also known by his Germanic name Kauffmann, was a 17th-century mathematician....
, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Gregory Saint-Vincent. It was first published by Mercator, in his 1668 treatise Logarithmo-technica.
Derivation
The series can be obtained from Taylor's theoremTaylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
, by inductively computing the nth derivative of ln x at x = 1, starting with
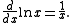
Alternatively, one can start with the finite geometric series (t ≠ −1)
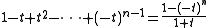
which gives

It follows that

and by termwise integration,
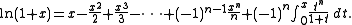
If −1 < x ≤ 1, the remainder term tends to 0 as
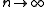 .
.This expression may be integrated iteratively k more times to yield
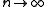
where
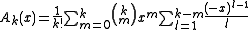
and
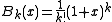
are polynomials in x.
Special cases
Setting x = 1 in the Mercator series yields the alternating harmonic series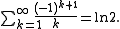
Complex series
The complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
power series
is the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for ln(1 + z), where ln denotes the principal branch
Principal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the complex logarithm
Complex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
. This series converges within the open unit disk |z| < 1 and on the circle |z| = 1 except at z = -1 (due to Abel's test), and the convergence is uniform on each closed disk of radius strictly less than 1.