
Method of moments (probability theory)
Encyclopedia
In probability theory
, the method of moments is a way of proving convergence in distribution by proving convergence of a sequence of moment
sequences. Suppose X is a random variable
and that all of the moments
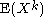
exist. Further suppose the probability distribution
of X is completely determined by its moments, i.e., there is no other probability distribution with the same sequence of moments
(cf. the problem of moments). If
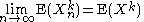
for all values of k, then the sequence {Xn} converges to X in distribution.
The method of moments was introduced by Pafnuty Chebyshev
for proving the central limit theorem
; Chebyshev cited earlier contributions by Irénée-Jules Bienaymé
. More recently, it has been applied by Eugene Wigner to prove Wigner's semicircle law, and has since found numerous applications in the theory of random matrices.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the method of moments is a way of proving convergence in distribution by proving convergence of a sequence of moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
sequences. Suppose X is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
and that all of the moments
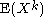
exist. Further suppose the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of X is completely determined by its moments, i.e., there is no other probability distribution with the same sequence of moments
(cf. the problem of moments). If
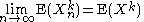
for all values of k, then the sequence {Xn} converges to X in distribution.
The method of moments was introduced by Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
for proving the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
; Chebyshev cited earlier contributions by Irénée-Jules Bienaymé
Irénée-Jules Bienaymé
Irénée-Jules Bienaymé , was a French statistician. He built on the legacy of Laplace generalizing his least squares method. He contributed to the fields and probability, and statistics and to their application to finance, demography and social sciences...
. More recently, it has been applied by Eugene Wigner to prove Wigner's semicircle law, and has since found numerous applications in the theory of random matrices.

