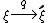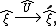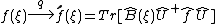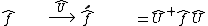Method of quantum characteristics
Encyclopedia
In quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization
through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta. These trajectories obey the Hamilton’s equations in quantum form and play the role of characteristics
in terms of which time-dependent Weyl's symbols of quantum operators can be expressed. In classical limit, quantum characteristics turn to classical trajectories. The knowledge of quantum characteristics is equivalent to the knowledge of quantum dynamics.
classical systems with degrees of freedom are described by
degrees of freedom are described by 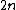 canonical coordinates and momenta
canonical coordinates and momenta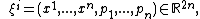
that form a coordinate system in the phase space. These variables satisfy the Poisson bracket
relations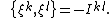
The skew-symmetric matrix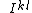 ,
,
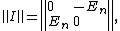
where is the
is the  identity matrix, defines nondegenerate 2-form in the phase space.
identity matrix, defines nondegenerate 2-form in the phase space.
The phase space acquires thereby the structure of a symplectic manifold
. The phase space is not metric space, so distance between two points is not defined. The Poisson bracket of two functions can be interpreted as the oriented area of a parallelogram whose adjacent sides are gradients of these functions.
Rotations in Euclidean space
leave the distance between two points invariant.
Canonical transformations in symplectic manifold leave the areas invariant.
In quantum mechanics, the canonical variables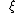 are associated to operators of canonical coordinates and momenta
are associated to operators of canonical coordinates and momenta
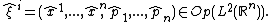
These operators act in Hilbert space
and obey commutation relations
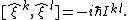
The Weyl’s association rule extends the correspondence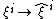 to arbitrary phase-space functions and operators.
to arbitrary phase-space functions and operators.
 was formulated by Weyl initially with the help of Taylor expansion
was formulated by Weyl initially with the help of Taylor expansion
of functions of operators of the canonical variables
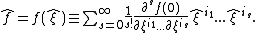
The operators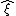 do not commute, so the Taylor expansion is not defined uniquely. The above prescription uses the symmetrized products of the operators. The real functions correspond to the Hermitian operators. The function
do not commute, so the Taylor expansion is not defined uniquely. The above prescription uses the symmetrized products of the operators. The real functions correspond to the Hermitian operators. The function 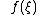 is called Weyl's symbol of operator
is called Weyl's symbol of operator 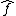 .
.
Under the reverse association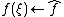 , the density matrix
, the density matrix
turns to Wigner function
. Wigner functions have numerous applications in quantum many-body physics, kinetic theory, collision theory, quantum chemistry.
A refined version of the Weyl-Wigner association rule is proposed by Stratonovich.
 -numbers and summation. Such a set constitutes a vector space
-numbers and summation. Such a set constitutes a vector space  . The association rule formulated with the use of the Taylor expansion preserves operations on the operators. The correspondence can be illustrated with the following diagram:
. The association rule formulated with the use of the Taylor expansion preserves operations on the operators. The correspondence can be illustrated with the following diagram:
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta. These trajectories obey the Hamilton’s equations in quantum form and play the role of characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
in terms of which time-dependent Weyl's symbols of quantum operators can be expressed. In classical limit, quantum characteristics turn to classical trajectories. The knowledge of quantum characteristics is equivalent to the knowledge of quantum dynamics.
Weyl-Wigner association rule
In Hamiltonian dynamicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
classical systems with
 degrees of freedom are described by
degrees of freedom are described by 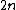 canonical coordinates and momenta
canonical coordinates and momenta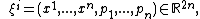
that form a coordinate system in the phase space. These variables satisfy the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
relations
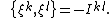
The skew-symmetric matrix
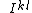 ,
,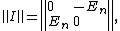
where
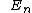 is the
is the  identity matrix, defines nondegenerate 2-form in the phase space.
identity matrix, defines nondegenerate 2-form in the phase space.The phase space acquires thereby the structure of a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. The phase space is not metric space, so distance between two points is not defined. The Poisson bracket of two functions can be interpreted as the oriented area of a parallelogram whose adjacent sides are gradients of these functions.
Rotations in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
leave the distance between two points invariant.
Canonical transformations in symplectic manifold leave the areas invariant.
In quantum mechanics, the canonical variables
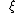 are associated to operators of canonical coordinates and momenta
are associated to operators of canonical coordinates and momenta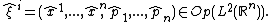
These operators act in Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and obey commutation relations
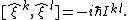
The Weyl’s association rule extends the correspondence
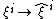 to arbitrary phase-space functions and operators.
to arbitrary phase-space functions and operators.Taylor expansion
A one-sided association rule was formulated by Weyl initially with the help of Taylor expansion
was formulated by Weyl initially with the help of Taylor expansionTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of functions of operators of the canonical variables
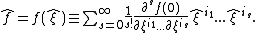
The operators
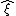 do not commute, so the Taylor expansion is not defined uniquely. The above prescription uses the symmetrized products of the operators. The real functions correspond to the Hermitian operators. The function
do not commute, so the Taylor expansion is not defined uniquely. The above prescription uses the symmetrized products of the operators. The real functions correspond to the Hermitian operators. The function 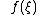 is called Weyl's symbol of operator
is called Weyl's symbol of operator 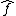 .
.Under the reverse association
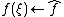 , the density matrix
, the density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
turns to Wigner function
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
. Wigner functions have numerous applications in quantum many-body physics, kinetic theory, collision theory, quantum chemistry.
A refined version of the Weyl-Wigner association rule is proposed by Stratonovich.
Stratonovich basis
The set of operators acting in the Hilbert space is closed under multiplication of operators by -numbers and summation. Such a set constitutes a vector space
-numbers and summation. Such a set constitutes a vector space 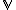 . The association rule formulated with the use of the Taylor expansion preserves operations on the operators. The correspondence can be illustrated with the following diagram:
. The association rule formulated with the use of the Taylor expansion preserves operations on the operators. The correspondence can be illustrated with the following diagram:
-
-
-
-
-
-
-
-
-
-
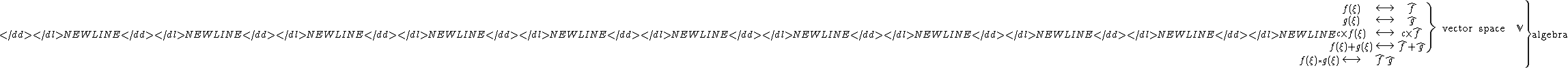
Here,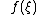 and
and 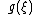 are functions and
are functions and 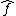 and
and 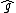 are the associated operators.
are the associated operators.
The elements of basis of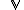 are labelled by canonical variables
are labelled by canonical variables 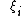 . The commonly used Stratonovich basis looks like
. The commonly used Stratonovich basis looks like
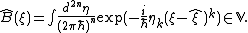
The Weyl-Wigner two-sided association rule for function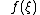 and operator
and operator 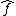 has the form
has the form
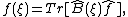
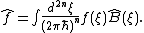
The function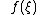 provides coordinates of the operator
provides coordinates of the operator  in the basis
in the basis  . The basis is complete and orthogonal:
. The basis is complete and orthogonal: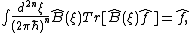
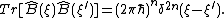
Alternative operator bases are discussed also. The freedom in
choice of the operator basis is better known as operator ordering problem.
Star-product
The set of operators is closed under the multiplication of operators. The vector space
is closed under the multiplication of operators. The vector space  is endowed thereby with an associative algebra structure. Given two functions
is endowed thereby with an associative algebra structure. Given two functions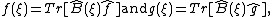
one can construct a third function

called -product
-product
or Moyal productMoyal productIn mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
. It is given explicitly by

where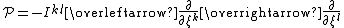
is the Poisson operator. The -product splits into symmetric and skew-symmetric parts
-product splits into symmetric and skew-symmetric parts

The -product is not associative. In the classical limit
-product is not associative. In the classical limit  -product becomes the dot-product. The skew-symmetric part
-product becomes the dot-product. The skew-symmetric part 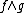 is known under the name of Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
is known under the name of Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
. This is the Weyl's symbol of commutator. In the classical limit Moyal bracket becomes Poisson bracket. Moyal bracket is quantum deformationDeformation theoryIn mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of Poisson bracket.
Quantum characteristics
The correspondence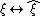 shows that coordinate transformations in the phase space are accompanied by transformations of operators of the canonical coordinates and momenta and vice versa. Let
shows that coordinate transformations in the phase space are accompanied by transformations of operators of the canonical coordinates and momenta and vice versa. Let 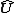 be the evolution operator,
be the evolution operator,
and is Hamiltonian. Consider the following scheme:
is Hamiltonian. Consider the following scheme:
Quantum evolution transforms vectors in the Hilbert space and, upon the Wigner association rule, coordinates in the phase space. In Heisenberg representationHeisenberg pictureIn physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
, the operators of the canonical variables are transformed as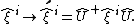
The phase-space coordinates that correspond to new operators
that correspond to new operators 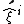 in the old basis
in the old basis 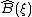 are given by
are given by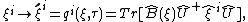
with the initial conditions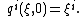
The functions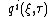 define quantum phase flow. In the general case, it is canonical to first order in
define quantum phase flow. In the general case, it is canonical to first order in  .
.
Star-function
The set of operators of canonical variables is complete in the sense that any operator can be represented as a function of operators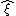 . Transformations
. Transformations
induce under the Wigner association rule transformations of phase-space functions:
Using the Taylor expansion, the transformation of function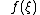 under the evolution can be found to be
under the evolution can be found to be
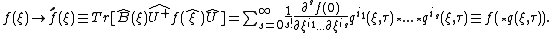
Composite function defined in such a way is called -function.
-function.
The composition law differs from the classical one. However, semiclassical expansion of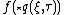 around
around  is formally well defined and involves even powers of
is formally well defined and involves even powers of  only.
only.
This equation shows that, given quantum characteristics are constructed, physical observables can be found without further addressing to Hamiltonian.
The functions play the role of characteristics similarly to classical characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
play the role of characteristics similarly to classical characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
used to solve classical Liouville equationLiouville's theorem (Hamiltonian)In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
.
Quantum Liouville equation
Wigner transform of the evolution equation for the density matrix in the Schrödinger representation leads quantum Liouville equation for the Wigner function. Wigner transform of the evolution equation for operators
in the Heisenberg representation,
leads to the same equation with the opposite (plus) sign in the right-hand side:
 -function solves this equation in terms of quantum characteristics:
-function solves this equation in terms of quantum characteristics: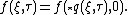
Similarly, the evolution of the Wigner function in the Schrödinger representation is given by
Quantum Hamilton's equations
Quantum Hamilton's equations can be obtained applying the Wigner transform to the evolution equations for Heisenberg operators of canonical coordinates and momenta
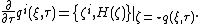
The right-hand side is calculated like in the classical mechanics. The composite function is, however, -function. The
-function. The  -product violates canonicity of the phase flow beyond the first order in
-product violates canonicity of the phase flow beyond the first order in  .
.
Conservation of Moyal bracket
The antisymmetrized products of even number of operators of canonical variables are c-numbers as a consequence
of the commutation relations. These products are left invariant by unitary transformations and, in particular,
Phase-space transformations induced by the evolution operator preserve the Moyal bracket and do not preserve the Poisson bracket, so the evolution map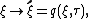
is not canonical. Transformation properties of canonical variables and phase-space functions under unitary transformations in the Hilbert space have important distinctions from the case of canonical transformations in the phase space:
Composition law
Quantum characteristics can hardly be treated visually as trajectories along which physical particles move. The reason lies in the star-composition law
which is non-local and is distinct from the dot-composition law of classical mechanics.
Energy conservation
The energy conservation implies ,
,
where
is Hamilton's function. In the usual geometric sense,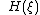 is not conserved along quantum characteristics.
is not conserved along quantum characteristics.
Summary
Table compares properties of characteristics in classical and quantum mechanics. PDE and ODE are partial differential equationsPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
and ordinary differential equationsOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, respectively. The quantum Liouville equation is the Weyl-Wigner transform of the von Neumann evolution equation for the density matrix in Schrödinger representationSchrödinger pictureIn physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
. The quantum Hamilton's equations are the Weyl-Wigner transforms of the evolution equations for operators of the canonical coordinates and momenta in Heisenberg representationHeisenberg pictureIn physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
.
In classical systems, characteristics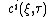 satisfy usually first-order ODE, e.g., classical Hamilton's equations, and solve first-order PDE, e.g., classical Liouville equation. Functions
satisfy usually first-order ODE, e.g., classical Hamilton's equations, and solve first-order PDE, e.g., classical Liouville equation. Functions  are characteristics also, despite both
are characteristics also, despite both 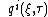 and
and 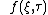 obey infinite-order PDE.
obey infinite-order PDE.
-
-
-
-
-
-
-
-
-
- {| class="wikitable"
-
-
-
-
-
-
-
-
|-
!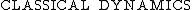
!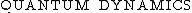
|-
| Liouville equation
|
|-
| Finite-order PDE
| Infinite-order PDE
|-
|
|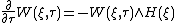
|-
| Hamilton's equations
|
|-
| Finite-order ODE
| Infinite-order PDE
|-
|
|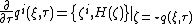
|-
| Initial conditions
| Initial conditions
|-
|
|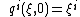
|-
| Composition law
| -composition law
-composition law
|-
|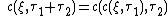
|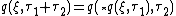
|-
| Conservation of Poisson bracket
| Conservation of Moyal bracket
|-
|
|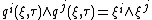
|-
| Energy conservation
| Energy conservation
|-
|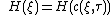
|
|-
| Solutions to Liouville equation
|
|-
|
|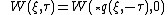
|}
The quantum phase flow contains entire information on the quantum evolution. Semiclassical expansion of quantum characteristics and -functions of quantum characteristics in power series in
-functions of quantum characteristics in power series in  allows calculation of the average values of time-dependent physical observables by solving a finite-order coupled system of ODE for phase space trajectories and Jacobi fields. The order of the system of ODE depends on truncation of the power series. The tunneling effect is nonperturbative in
allows calculation of the average values of time-dependent physical observables by solving a finite-order coupled system of ODE for phase space trajectories and Jacobi fields. The order of the system of ODE depends on truncation of the power series. The tunneling effect is nonperturbative in 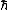 and is not captured by the expansion. Quantum characteristics are distinct from trajectories of the de Broglie - Bohm theory.
and is not captured by the expansion. Quantum characteristics are distinct from trajectories of the de Broglie - Bohm theory.
See also
- Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
- Wigner distribution functionWigner distribution functionThe Wigner distribution function was first proposed to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution....
- Modified Wigner distribution functionModified Wigner distribution functionThe Wigner distribution was first proposed for corrections to classical statistical mechanics in 1932 by Eugene Wigner. The Wigner distribution, or Wigner–Ville distribution for analytic signals, also has applications in time frequency analysis...
- Negative probabilityNegative probabilityIn 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" where he introduced the concept of negative energies and negative probabilities:...
- Method of characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
Textbooks
- H. Weyl, The Theory of Groups and Quantum Mechanics, (Dover Publications, New York Inc., 1931).
- V. I. Arnold, Mathematical Methods of Classical Mechanics, (2-nd ed. Springer-Verlag, New York Inc., 1989).
- M. V. Karasev and V. P Maslov, Nonlinear Poisson Brackets, (Nauka, Moscow, 1991).
-
-
-
-
-
-
-
-
-
-