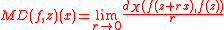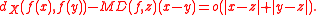Metric differential
Encyclopedia
In mathematical analysis
, a metric differential is a generalization of a derivative
for a Lipschitz continuous function
defined on a Euclidean space
and taking values in an arbitrary metric space
. With this definition of a derivative, one can generalize Rademarcher's theorem
to metric space-valued Lipschitz functions.
states that a Lipschitz map f : Rn → Rm is differentiable amost everywhere in Rn; in other words, for almost every x, f is approximately linear when you look in a small enough neighborhood of x. If f is a function from a Euclidean space Rn that takes values instead in a metric space
X, it doesn't immediately make sense to talk about differentiability since X has no linear structure a priori. Even if you assume that X is a Banach space
and ask whether a Fréchet derivative
exists almost everywhere, this does not hold. For example, consider the function f : [0,1] → L1([0,1]), mapping the unit interval into the space of integrable functions
, defined by f(x) = χ[0,x], this function is Lipschitz (and in fact, an isometry
) since, if 0 ≤ x ≤ y≤ 1, then
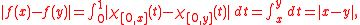
but one can verify that limh→0(f(x + h) − f(x))/h does not converge to an L1 function for any x in [0,1], so it is not differentiable anywhere.
However, if you look at Rademacher's theorem as a statement about how a Lipschitz function stabilizes as you zoom in on almost every point, then such a theorem exists but is stated in terms of the metric properties of f instead of its linear properties.
whenever the limit exists (here d X denotes the metric on X).
A theorem due to Bernd Kirchheim states that a Rademacher theorem in terms of metric differentials holds: for almost every z in Rm, MD(f, z) is a seminorm and
What this little-o notation means is that, at values very close to z, the function f is approximately an isometry
from Rn with respect to the seminorm MD(f, z) into the metric space X.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a metric differential is a generalization of a derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
for a Lipschitz continuous function
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
defined on a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and taking values in an arbitrary metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. With this definition of a derivative, one can generalize Rademarcher's theorem
Rademacher's theorem
In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
to metric space-valued Lipschitz functions.
Discussion
Rademacher's theoremRademacher's theorem
In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
states that a Lipschitz map f : Rn → Rm is differentiable amost everywhere in Rn; in other words, for almost every x, f is approximately linear when you look in a small enough neighborhood of x. If f is a function from a Euclidean space Rn that takes values instead in a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X, it doesn't immediately make sense to talk about differentiability since X has no linear structure a priori. Even if you assume that X is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and ask whether a Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
exists almost everywhere, this does not hold. For example, consider the function f : [0,1] → L1([0,1]), mapping the unit interval into the space of integrable functions
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, defined by f(x) = χ[0,x], this function is Lipschitz (and in fact, an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
) since, if 0 ≤ x ≤ y≤ 1, then
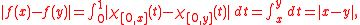
but one can verify that limh→0(f(x + h) − f(x))/h does not converge to an L1 function for any x in [0,1], so it is not differentiable anywhere.
However, if you look at Rademacher's theorem as a statement about how a Lipschitz function stabilizes as you zoom in on almost every point, then such a theorem exists but is stated in terms of the metric properties of f instead of its linear properties.
Definition and existence of the metric differential
A substitute for a derivative of f:Rn → X is the metric differential of f at a point z in Rmn which is a function on Rm defined by the limitwhenever the limit exists (here d X denotes the metric on X).
A theorem due to Bernd Kirchheim states that a Rademacher theorem in terms of metric differentials holds: for almost every z in Rm, MD(f, z) is a seminorm and
What this little-o notation means is that, at values very close to z, the function f is approximately an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
from Rn with respect to the seminorm MD(f, z) into the metric space X.