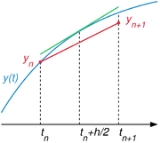
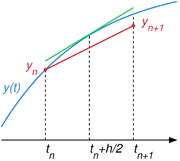
Midpoint method
Encyclopedia
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, a branch of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, the midpoint method is a one-step method for solving the differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
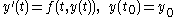
numerically
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
, and is given by the formula
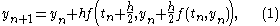
for
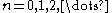 Here,
Here, 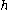 is the step size — a small positive number,
is the step size — a small positive number, 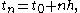 and
and 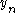 is the computed approximate value of
is the computed approximate value of 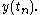
The name of the method comes from the fact that in the formula above the function
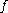 is evaluated at
is evaluated at 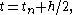 which is the midpoint between
which is the midpoint between 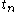 at which the value of y(t) is known and
at which the value of y(t) is known and 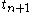 at which the value of y(t) needs to be found.
at which the value of y(t) needs to be found.The error at each step of the midpoint method is of order
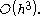 Thus, while more computationally intensive than Euler's method, the midpoint method generally gives more accurate results.
Thus, while more computationally intensive than Euler's method, the midpoint method generally gives more accurate results.The method is an example of a class of higher-order methods known as Runge-Kutta methods.
Derivation of the midpoint method
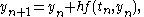
and is derived in a similar manner.
The key to deriving Euler's method is the approximate equality
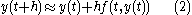
which is obtained from the slope formula
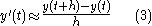
and keeping in mind that
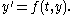
For the midpoint method, one replaces (3) with the more accurate
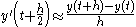
when instead of (2) we find
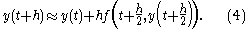
One cannot use this equation to find
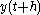 as one does not know
as one does not know 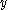 at
at 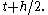 The solution is then to use a Taylor series
The solution is then to use a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion exactly as if using the Euler method to solve for
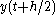 :
: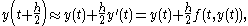
which, when plugged in (4), gives us
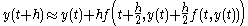
and the midpoint method (1).
See also
- Rectangle methodRectangle methodIn mathematics, specifically in integral calculus, the rectangle method computes an approximation to a definite integral, made by finding the area of a collection of rectangles whose heights are determined by the values of the function.Specifically, the interval over which the function is to be...
- Heun's methodHeun's methodIn mathematics and computational science, Heun's method may refer to the improved or modified Euler's method , or a similar two-stage Runge–Kutta method. It is named after Karl L. W. M. Heun and is a numerical procedure for solving ordinary differential equations with a given initial value...
- Leapfrog integrationLeapfrog integrationLeapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...
and Verlet integrationVerlet integrationVerlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics...

