Minimum degree algorithm
Encyclopedia
In numerical analysis
the minimum degree algorithm is an algorithm
used to permute the rows and columns of a symmetric sparse matrix
before applying the Cholesky decomposition
, to reduce the number of non-zeros in the Cholesky factor.
This results in reduced storage requirements and means that the Cholesky factor, or sometimes an incomplete Cholesky factor used as a preconditioner (for example in the preconditioned conjugate gradient algorithm) can be applied with fewer arithmetic operations.
Minimum degree algorithms are often used in the finite element method
where the reordering of nodes can be carried out depending only on the topology of the mesh, rather than the coefficients in the partial differential equation, resulting in efficiency savings when the same mesh is used for a variety of coefficient values.
Given a linear system
where A is an
real symmetric sparse square matrix the Cholesky factor L will typically suffer 'fill in', that is have more non-zeros than the upper triangle of A. We seek a permutation matrix
P , so that the matrix
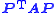, which is also symmetric, has the least possible fill in its Cholesky factor. We solve the reordered system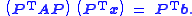
The problem of finding the best ordering is an NP-complete
problem and is thus intractable, so heuristic methods are used instead. The minimum degree algorithm is derived from a method first proposed by Markowitz
in 1959 for non-symmetric linear programming
problems, which is loosely described as follows. At each step in Gaussian elimination
row and column permutations are performed so as to minimize the number of off diagonal non-zeros in the pivot row and column. A symmetric version
of Markowitz method was described by Tinney and Walker in 1967 and Rose later derived a graph theoretic version of the algorithm where the factorization is only simulated, and this was named the minimum degree algorithm. The graph referred to is the graph with n vertices, with vertices i and j connected by an edge when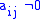
, and the degree is the degree of the vertices. A crucial aspect of such algorithms is a tie breaking strategy when there is a choice of renumbering resulting in the same degree.
A version of the minimum degree algorithm was implemented in the MATLAB
function symmmd, but has now been superseded by a symmetric approximate multiple minimum degree function symamd, which is faster.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
the minimum degree algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used to permute the rows and columns of a symmetric sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
before applying the Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
, to reduce the number of non-zeros in the Cholesky factor.
This results in reduced storage requirements and means that the Cholesky factor, or sometimes an incomplete Cholesky factor used as a preconditioner (for example in the preconditioned conjugate gradient algorithm) can be applied with fewer arithmetic operations.
Minimum degree algorithms are often used in the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
where the reordering of nodes can be carried out depending only on the topology of the mesh, rather than the coefficients in the partial differential equation, resulting in efficiency savings when the same mesh is used for a variety of coefficient values.
Given a linear system
where A is an
real symmetric sparse square matrix the Cholesky factor L will typically suffer 'fill in', that is have more non-zeros than the upper triangle of A. We seek a permutation matrixPermutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
P , so that the matrix
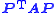, which is also symmetric, has the least possible fill in its Cholesky factor. We solve the reordered system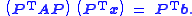The problem of finding the best ordering is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem and is thus intractable, so heuristic methods are used instead. The minimum degree algorithm is derived from a method first proposed by Markowitz
Harry Markowitz
Harry Max Markowitz is an American economist and a recipient of the John von Neumann Theory Prize and the Nobel Memorial Prize in Economic Sciences....
in 1959 for non-symmetric linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problems, which is loosely described as follows. At each step in Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
row and column permutations are performed so as to minimize the number of off diagonal non-zeros in the pivot row and column. A symmetric version
of Markowitz method was described by Tinney and Walker in 1967 and Rose later derived a graph theoretic version of the algorithm where the factorization is only simulated, and this was named the minimum degree algorithm. The graph referred to is the graph with n vertices, with vertices i and j connected by an edge when
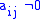, and the degree is the degree of the vertices. A crucial aspect of such algorithms is a tie breaking strategy when there is a choice of renumbering resulting in the same degree.A version of the minimum degree algorithm was implemented in the MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
function symmmd, but has now been superseded by a symmetric approximate multiple minimum degree function symamd, which is faster.