
Minimum distance estimation
Encyclopedia
Minimum distance estimation (MDE) is a statistical method for fitting a mathematical model to data, usually the empirical distribution
.
 be an independent and identically distributed (iid) random
be an independent and identically distributed (iid) random
sample
from a population
with distribution
 and
and 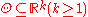 .
.
Let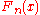 be the empirical distribution function
be the empirical distribution function
based on the sample.
Let be an estimator
be an estimator
for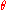 . Then
. Then  is an estimator for
is an estimator for 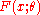 .
.
Let be a functional
be a functional
returning some measure of "distance" between the two arguments. The functional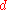 is also called the criterion function.
is also called the criterion function.
If there exists a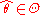 such that
such that 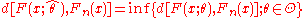 , then
, then 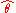 is called the minimum distance estimate of
is called the minimum distance estimate of 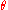 .
.
tests: the test statistic used in one of these tests is used as the distance measure to be minimised. Below are some examples of statistical tests that have been used for minimum distance estimation.
of the absolute difference
between the empirical and the estimated distribution functions.
tests. Often the cases of the Cramér–von Mises criterion, the Kolmogorov–Smirnov test and the Anderson–Darling test are treated simultaneously by treating them as special cases of a more general formulation of a distance measure. Examples of the theoretical results that are available are: consistency
of the parameter estimates; the asymptotic covariance matrices of the parameter estimates.
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
.
Definition
Let be an independent and identically distributed (iid) random
be an independent and identically distributed (iid) randomRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
sample
Random sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...
from a population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
with distribution
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
 and
and 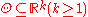 .
.Let
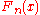 be the empirical distribution function
be the empirical distribution functionEmpirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
based on the sample.
Let
 be an estimator
be an estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
for
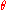 . Then
. Then  is an estimator for
is an estimator for 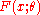 .
.Let
 be a functional
be a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
returning some measure of "distance" between the two arguments. The functional
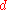 is also called the criterion function.
is also called the criterion function.If there exists a
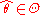 such that
such that 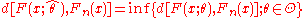 , then
, then 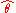 is called the minimum distance estimate of
is called the minimum distance estimate of 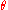 .
.Statistics used in estimation
Most theoretical studies of minimum distance estimation, and most applications, make use of "distance" measures which underlie already-established goodness of fitGoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
tests: the test statistic used in one of these tests is used as the distance measure to be minimised. Below are some examples of statistical tests that have been used for minimum distance estimation.
Chi-square criterion
The chi-square test uses as its criterion the sum, over predefined groups, of the squared difference between the increases of the empirical distribution and the estimated distribution, weighted by the increase in the estimate for that group.Cramér–von Mises criterion
The Cramér–von Mises criterion uses the integral of the squared difference between the empirical and the estimated distribution functions.Kolmogorov–Smirnov criterion
The Kolmogorov–Smirnov test uses the supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
between the empirical and the estimated distribution functions.
Anderson–Darling criterion
The Anderson–Darling test is similar to the Cramér–von Mises criterion except that the integral is of a weighted version of the squared difference, where the weighting relates the variance of the empirical distribution function.Theoretical results
The theory of minimum distance estimation is related to that for the asymptotic distribution of the corresponding statistical goodness of fitGoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
tests. Often the cases of the Cramér–von Mises criterion, the Kolmogorov–Smirnov test and the Anderson–Darling test are treated simultaneously by treating them as special cases of a more general formulation of a distance measure. Examples of the theoretical results that are available are: consistency
Consistency (statistics)
In statistics, consistency of procedures such as confidence intervals or hypothesis tests involves their behaviour as the number of items in the data-set to which they are applied increases indefinitely...
of the parameter estimates; the asymptotic covariance matrices of the parameter estimates.
See also
- Maximum likelihood estimation
- Maximum spacing estimationMaximum spacing estimationIn statistics, maximum spacing estimation , or maximum product of spacing estimation , is a method for estimating the parameters of a univariate statistical model...

