Goodness of fit
Encyclopedia
The goodness of fit of a statistical model
describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing
, e.g. to test for normality
of residual
s, to test whether two samples are drawn from identical distributions (see Kolmogorov–Smirnov test), or whether outcome frequencies follow a specified distribution (see Pearson's chi-squared test
). In the analysis of variance
, one of the components into which the variance is partitioned may be a lack-of-fit sum of squares
.
, the following topics relate to goodness of fit:
where
is the known variance
of the observation, O is the observed data and E is the theoretical data. This definition is only useful when one has estimates for the error on the measurements, but it leads to a situation where a chi-squared distribution can be used to test goodness of fit, provided that the errors can be assumed to have a normal distribution.
The reduced chi-squared statistic is simply the chi-squared divided by the number of degrees of freedom
:
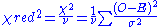
where
is the number of degrees of freedom
, usually given by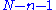
, where 
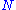is the number of observations, and 
is the number of fitted parameters, assuming that the mean value is an additional fitted parameter. The advantage of the reduced chi-squared is that it already normalizes for the number of data points and model complexity.
As a rule of thumb, a large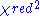
indicates a poor model fit. However 
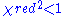indicates that the model is 'over-fitting' the data (either the model is improperly fitting noise, or the error variance has been over-estimated). A 
indicates that the fit has not fully captured the data (or that the error variance has been under-estimated). In principle a value of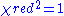 
indicates that the extent of the match between observations and estimates is in accord with the error variance.
uses a measure of goodness of fit which is the sum of differences between observed and expected outcome
frequencies (that is, counts of observations), each squared and divided by the expectation:
where:
The expected frequency is calculated by: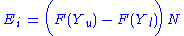
where:
The resulting value can be compared to the chi-squared distribution to determine the goodness of fit. In order to determine the degrees of freedom
of the chi-squared distribution, one takes the total number of observed frequencies and subtracts one. The test statistic follows, approximately, a chi-square distribution with (k − c) degrees of freedom where k is the number of non-empty cells and c is the number of estimated parameters (including location and scale parameters and shape parameters) for the distribution + 1. For example, for a 3-parameter Weibull distribution, c = 4.
If the null hypothesis is true (i.e., men and women are chosen with equal probability in the sample), the test statistic will be drawn from a chi-squared distribution with one degree of freedom
. Though one might expect two degrees of freedom (one each for the men and women), we must take into account that the total number of men and women is constrained (100), and thus there is only one degree of freedom (2 − 1). Alternatively, if the male count is known the female count is determined, and vice-versa.
Consultation of the chi-squared distribution for 1 degree of freedom shows that the probability
of observing this difference (or a more extreme difference than this) if men and women are equally numerous in the population is approximately 0.23. This probability is higher than conventional criteria for statistical significance
(.001-.05), so normally we would not reject the null hypothesis that the number of men in the population is the same as the number of women (i.e. we would consider our sample within the range of what we'd expect for a 50/50 male/female ratio.)
This has approximately a chi-squared distribution with k − 1 df. The fact that df = k − 1 is a consequence of the restriction
. We know there are k observed cell counts, however, once any k − 1 are known, the remaining one is uniquely determined. Basically, one can say, there are only k − 1 freely determined cell counts, thus df = k − 1.
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
, e.g. to test for normality
Normality test
In statistics, normality tests are used to determine whether a data set is well-modeled by a normal distribution or not, or to compute how likely an underlying random variable is to be normally distributed....
of residual
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
s, to test whether two samples are drawn from identical distributions (see Kolmogorov–Smirnov test), or whether outcome frequencies follow a specified distribution (see Pearson's chi-squared test
Pearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
). In the analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
, one of the components into which the variance is partitioned may be a lack-of-fit sum of squares
Lack-of-fit sum of squares
In statistics, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance, used in the numerator in an F-test of the null hypothesis that says that a proposed model fits well.- Sketch of...
.
Fit of distributions
In assessing whether a given distribution is suited to a data-set, the following tests and their underlying measures of fit can be used:- Kolmogorov–Smirnov test;
- Cramér–von Mises criterion;
- Anderson–Darling test;
- Chi Square test;
Regression analysis
In regression analysisRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, the following topics relate to goodness of fit:
- Coefficient of determinationCoefficient of determinationIn statistics, the coefficient of determination R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model...
(The R squared measure of goodness of fit); - Lack-of-fit sum of squaresLack-of-fit sum of squaresIn statistics, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance, used in the numerator in an F-test of the null hypothesis that says that a proposed model fits well.- Sketch of...
.
Example
One way in which a measure of goodness of fit statistic can be constructed, in the case where the variance of the measurement error is known, is to construct a weighted sum of squared errors:where
is the known varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the observation, O is the observed data and E is the theoretical data. This definition is only useful when one has estimates for the error on the measurements, but it leads to a situation where a chi-squared distribution can be used to test goodness of fit, provided that the errors can be assumed to have a normal distribution.
The reduced chi-squared statistic is simply the chi-squared divided by the number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
:
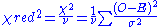
where
is the number of degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
, usually given by
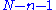, where 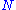is the number of observations, and is the number of fitted parameters, assuming that the mean value is an additional fitted parameter. The advantage of the reduced chi-squared is that it already normalizes for the number of data points and model complexity.As a rule of thumb, a large
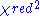indicates a poor model fit. However 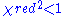indicates that the model is 'over-fitting' the data (either the model is improperly fitting noise, or the error variance has been over-estimated). A indicates that the fit has not fully captured the data (or that the error variance has been under-estimated). In principle a value of 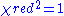indicates that the extent of the match between observations and estimates is in accord with the error variance.Pearson's chi-squared test
Pearson's chi-squared testPearson's chi-squared test
Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
uses a measure of goodness of fit which is the sum of differences between observed and expected outcome
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
frequencies (that is, counts of observations), each squared and divided by the expectation:
where:
- Oi = an observed frequency (i.e. count) for bin i
- Ei = an expected (theoretical) frequency for bin i, asserted by the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
.
The expected frequency is calculated by:
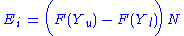
where:
- F = the cumulative Distribution function for the distribution being tested.
- Yu = the upper limit for class i,
- Yl = the lower limit for class i, and
- N = the sample size
The resulting value can be compared to the chi-squared distribution to determine the goodness of fit. In order to determine the degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
of the chi-squared distribution, one takes the total number of observed frequencies and subtracts one. The test statistic follows, approximately, a chi-square distribution with (k − c) degrees of freedom where k is the number of non-empty cells and c is the number of estimated parameters (including location and scale parameters and shape parameters) for the distribution + 1. For example, for a 3-parameter Weibull distribution, c = 4.
Example: equal frequencies of men and women
For example, to test the hypothesis that a random sample of 100 people has been drawn from a population in which men and women are equal in frequency, the observed number of men and women would be compared to the theoretical frequencies of 50 men and 50 women. If there were 44 men in the sample and 56 women, thenIf the null hypothesis is true (i.e., men and women are chosen with equal probability in the sample), the test statistic will be drawn from a chi-squared distribution with one degree of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
. Though one might expect two degrees of freedom (one each for the men and women), we must take into account that the total number of men and women is constrained (100), and thus there is only one degree of freedom (2 − 1). Alternatively, if the male count is known the female count is determined, and vice-versa.
Consultation of the chi-squared distribution for 1 degree of freedom shows that the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of observing this difference (or a more extreme difference than this) if men and women are equally numerous in the population is approximately 0.23. This probability is higher than conventional criteria for statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
(.001-.05), so normally we would not reject the null hypothesis that the number of men in the population is the same as the number of women (i.e. we would consider our sample within the range of what we'd expect for a 50/50 male/female ratio.)
Binomial case
A binomial experiment is a sequence of independent trials in which the trials can result in one of two outcomes, success or failure. There are n trials each with probability of success, denoted by p. Provided that npi ≫ 1 for every i (where i = 1, 2, ..., k), thenThis has approximately a chi-squared distribution with k − 1 df. The fact that df = k − 1 is a consequence of the restriction
. We know there are k observed cell counts, however, once any k − 1 are known, the remaining one is uniquely determined. Basically, one can say, there are only k − 1 freely determined cell counts, thus df = k − 1.