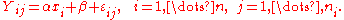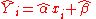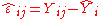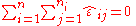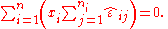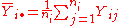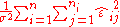Lack-of-fit sum of squares
Encyclopedia
In statistics
, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance
, used in the numerator in an F-test
of the null hypothesis
that says that a proposed model fits well.
value of the response variable for each value of the set of predictor variables. For example, consider fitting a line
by the method of least squares
. One takes as estimates of α and β the values that minimize the sum of squares of residuals
, i.e., the sum of squares of the differences between the observed y-value and the fitted y-value. To have a lack-of-fit sum of squares, one observes more than one y-value for each x-value. One then partitions the "sum of squares due to error", i.e., the sum of squares of residuals, into two components:
The sum of squares due to "pure" error is the sum of squares of the differences between each observed y-value and the average of all y-values corresponding to the same x-value.
The sum of squares due to lack of fit is the weighted sum of squares of differences between each average of y-values corresponding to the same x-value and corresponding fitted y-value, the weight in each case being simply the number of observed y-values for that x-value.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
, used in the numerator in an F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
of the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that says that a proposed model fits well.
Sketch of the idea
In order to have a lack-of-fit sum of squares one observes more than oneReplication (statistics)
In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "the repetition of the set of all the treatment combinations to be compared in...
value of the response variable for each value of the set of predictor variables. For example, consider fitting a line
by the method of least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
. One takes as estimates of α and β the values that minimize the sum of squares of residuals
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
, i.e., the sum of squares of the differences between the observed y-value and the fitted y-value. To have a lack-of-fit sum of squares, one observes more than one y-value for each x-value. One then partitions the "sum of squares due to error", i.e., the sum of squares of residuals, into two components:
- sum of squares due to error = (sum of squares due to "pure" error) + (sum of squares due to lack of fit).
The sum of squares due to "pure" error is the sum of squares of the differences between each observed y-value and the average of all y-values corresponding to the same x-value.
The sum of squares due to lack of fit is the weighted sum of squares of differences between each average of y-values corresponding to the same x-value and corresponding fitted y-value, the weight in each case being simply the number of observed y-values for that x-value.
-
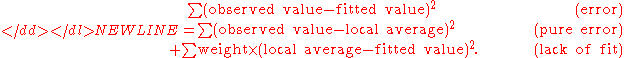
In order that these two sums be equal, it is necessary that the vector whose components are "pure errors" and the vector of lack-of-fit components be orthogonal to each other, and one may check that they are orthogonal by doing some algebra.
Mathematical details
Consider fitting a line, where i is an index of each unique x value, and j is an index of an observation for a given x value. The value of each observation can be represented by
Let
be the least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
estimates of the unobservable parameters α and β based on the observed values of x i and Y i j.
Let
be the fitted values of the response variable. Then
are the residualsErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
, which are observable estimates of the unobservable values of the error term ε ij. Because of the nature of the method of least squares, the whole vector of residuals, with

scalar components, necessarily satisfies the two constraints
It is thus constrained to lie in an (N − 2)-dimensional subspace of R N, i.e. there are N − 2 "degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
for error".
Now let
be the average of all Y-values associated with a particular x-value.
We partition the sum of squares due to error into two components:

Sums of squares
Suppose the error termsErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
ε i j are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
and normally distributed with expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0 and varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2. We treat x i as constant rather than random. Then the response variables Y i j are random only because the errors ε i j are random.
It can be shown to follow that if the straight-line model is correct, then the sum of squares due to error divided by the error variance,
has a chi-squared distribution with N − 2 degrees of freedom.
Moreover:
- The sum of squares due to pure error, divided by the error variance σ2, has a chi-squared distribution with N − n degrees of freedom;
- The sum of squares due to lack of fit, divided by the error variance σ2, has a chi-squared distribution with n − 2 degrees of freedom;
- The two sums of squares are probabilistically independent.
The test statistic
It then follows that the statistic
-
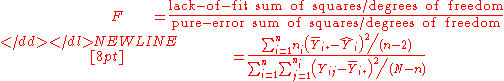
has an F-distribution with the corresponding number of degrees of freedom in the numerator and the denominator, provided that the straight-line model is correct. If the model is wrong, then the probability distribution of the denominator is still as stated above, and the numerator and denominator are still independent. But the numerator then has a noncentral chi-squared distribution, and consequently the quotient as a whole has a non-central F-distribution.
One uses this F-statistic to test the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
that the straight-line model is right. Since the non-central F-distribution is stochastically larger than the (central) F-distribution, one rejects the null hypothesis if the F-statistic is too big. How big is too big—the critical value—depends on the level of the test and is a percentage point of the F-distribution.
The assumptions of normal distribution of errors and statistical independenceStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
can be shown to entail that this lack-of-fit testLack-of-fit testIn statistics, a lack-of-fit test is any of many tests of a null hypothesis that a proposed statistical model fits well. See:* Goodness of fit* Lack-of-fit sum of squares...
is the likelihood-ratio testLikelihood-ratio testIn statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
of this null hypothesis.
-