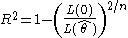Coefficient of determination
Encyclopedia
In statistics
, the coefficient of determination R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model. It provides a measure of how well future outcomes are likely to be predicted by the model.
There are several different definitions of R2 which are only sometimes equivalent. One class of such cases includes that of linear regression
. In this case, if an intercept is included then R2 is simply the square of the sample correlation coefficient
between the outcomes and their predicted values, or in the case of simple linear regression
, between the outcomes and the values of the single regressor being used for prediction. In such cases, the coefficient of determination ranges from 0 to 1. Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions which are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of R2 may occur when fitting non-linear trends to data. In these instances, the mean of the data provides a fit to the data that is superior to that of the trend under this goodness of fit
analysis.
The "variability" of the data set is measured through different sums of squares
:
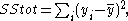the total sum of squares
(proportional to the sample variance);
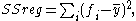the regression sum of squares, also called the explained sum of squares
.
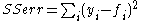, the sum of squares of residuals, also called the residual sum of squares
.
In the above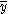
is the mean of the observed data:
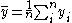
where n is the number of observations.
The notations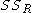
and 
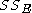should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
The most general definition of the coefficient of determination is
.
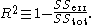
equals the sum of the two other sums of squares defined above,
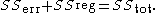
See sum of squares
for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of R2 is equivalent to
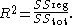
In this form R2 is given directly in terms of the explained variance: it compares the explained variance (variance of the model's predictions) with the total variance (of the data).
This partition of the sum of squares holds for instance when the model values ƒi have been obtained by linear regression
. A milder sufficient condition reads as follows: The model has the form
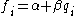
where the qi are arbitrary values that may or may not depend on i or on other free parameters (the common choice qi = xi is just one special case), and the coefficients α and β are obtained by minimizing the residual sum of squares.
This set of conditions is an important one and it has a number of implications for the properties of the fitted residuals
and the modelled values. In particular, under these conditions:
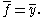
), R2 equals the square of the correlation coefficient
between the observed and modeled (predicted) data values.
Under general conditions, an R2 value is sometimes calculated as the square of the correlation coefficient
between the original and modeled data values. In this case, the value is not directly a measure of how good the modeled values are, but rather a measure of how good a predictor might be constructed from the modeled values (by creating a revised predictor of the form α + βƒi). According to Everitt (2002, p. 78), this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables.
of a model. In regression, the R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1.0 indicates that the regression line perfectly fits the data.
Values of R2 outside the range 0 to 1 can occur where it is used to measure the agreement between observed and modelled values and where the "modelled" values are not obtained by linear regression and depending on which formulation of R2 is used. If the first formula above is used, values can never be greater than one. If the second expression is used, there are no constraints on the values obtainable.
In many (but not all) instances where R2 is used, the predictors are calculated by ordinary least-squares regression: that is, by minimizing SSerr. In this case R-squared increases as we increase the number of variables in the model (R2 will not decrease). This illustrates a drawback to one possible use of R2, where one might try to include more variables in the model until "there is no more improvement". This leads to the alternative approach of looking at the adjusted R2. The explanation of this statistic is almost the same as R2 but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the R2 statistic can be calculated as above and may still be a useful measure. If fitting is by weighted least squares or generalized least squares
, alternative versions of R2 can be calculated appropriate to those statistical frameworks, while the "raw" R2 may still be useful if it is more easily interpreted. Values for R2 can be calculated for any type of predictive model, which need not have a statistical basis.
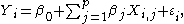
where, for the ith case,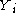
is the response variable, 
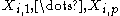are p regressors, and 
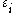is a mean zero error
term. The quantities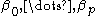
are unknown coefficients, whose values are determined by least squares
. The coefficient of determination R2 is a measure of the global fit of the model. Specifically, R2 is an element of [0, 1] and represents the proportion of variability in Yi that may be attributed to some linear combination of the regressors (explanatory variables) in X.
R2 is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, R2 = 1 indicates that the fitted model explains all variability in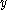
, while R2 = 0 indicates no 'linear' relationship (for straight line regression, this means that the straight line model is a constant line (slope=0, intercept=
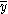) between the response variable and regressors). An interior value such as R2 = 0.7 may be interpreted as follows: "Approximately seventy percent of the variation in the response variable can be explained by the explanatory variable. The remaining thirty percent can be explained by unknown, lurking variable
s or inherent variability."
A caution that applies to R2, as to other statistical descriptions of correlation
and association is that "correlation does not imply causation
." In other words, while correlations may provide valuable clues regarding causal relationships among variables, a high correlation between two variables does not represent adequate evidence that changing one variable has resulted, or may result, from changes of other variables.
In case of a single regressor, fitted by least squares, R2 is the square of the Pearson product-moment correlation coefficient
relating the regressor and the response variable. More generally, R2 is the square of the correlation between the constructed predictor and the response variable.
regression, R2 is weakly increasing in the number of regressors in the model. As such, R2 alone cannot be used as a meaningful comparison of models with different numbers of independent variables. For a meaningful comparison between two models, an F-test
can be performed on the residual sum of squares
, similar to the F-tests in Granger causality
. As a reminder of this, some authors denote R2 by R2p, where p is the number of columns in X
To demonstrate this property, first recall that the objective of least squares regression is:
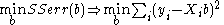
The optimal value of the objective is weakly smaller as additional columns of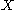
are added, by the fact that relatively unconstrained minimization leads to a solution which is weakly smaller than relatively constrained minimization. Given the previous conclusion and noting that 
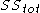depends only on y, the non-decreasing property of R2 follows directly from the definition above.
The intuitive reason that using an additional explanatory variable cannot lower the R2 is this: Minimizing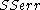
is equivalent to maximizing R2. When the extra variable is included, the data always have the option of giving it an estimated coefficient of zero, leaving the predicted values and the R2 unchanged. The only way that the optimization problem will give a non-zero coefficient is if doing so improves the R2.
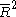and pronounced "R bar squared") is a modification due to Theil of R2 that adjusts for the number of explanatory terms in a model. Unlike R2, the adjusted R2 increases only if the new term improves the model more than would be expected by chance. The adjusted R2 can be negative, and will always be less than or equal to R2. The adjusted R2 is defined as
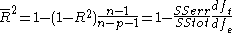
where p is the total number of regressors in the linear model (but not counting the constant term), n is the sample size, dft is the degrees of freedom
n– 1 of the estimate of the population variance of the dependent variable, and dfe is the degrees of freedom n – p – 1 of the estimate of the underlying population error variance.
The principle behind the Adjusted R2 statistic can be seen by rewriting the ordinary R2 as
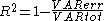
where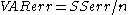
and 
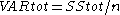are estimates of the variances of the errors and of the observations, respectively. These estimates are replaced by statistically unbiased versions: 
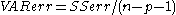and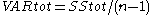 
.
Adjusted R2 does not have the same interpretation as R2. As such, care must be taken in interpreting and reporting this statistic. Adjusted R2 is particularly useful in the Feature selection
stage of model building..
The use of an adjusted R2 is an attempt to take account of the phenomenon of statistical shrinkage
.
The generalized R² has all of these properties.
where L(0) is the likelihood of the model with only the intercept,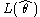
is the likelihood of the estimated model and n is the sample size.
However, in the case of a logistic model, where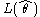
cannot be greater than 1, R² is between 0 and 
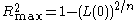: thus, it is possible to define a scaled R² as R²/R²max.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the coefficient of determination R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model. It provides a measure of how well future outcomes are likely to be predicted by the model.
There are several different definitions of R2 which are only sometimes equivalent. One class of such cases includes that of linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
. In this case, if an intercept is included then R2 is simply the square of the sample correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between the outcomes and their predicted values, or in the case of simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
, between the outcomes and the values of the single regressor being used for prediction. In such cases, the coefficient of determination ranges from 0 to 1. Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions which are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of R2 may occur when fitting non-linear trends to data. In these instances, the mean of the data provides a fit to the data that is superior to that of the trend under this goodness of fit
Goodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
analysis.
Definitions
A data set has values yi, each of which has an associated modelled value fi (also sometimes referred to as ŷi). Here, the values yi are called the observed values and the modelled values fi are sometimes called the predicted values.The "variability" of the data set is measured through different sums of squares
Sum of squares
The partition of sums of squares is a concept that permeates much of inferential statistics and descriptive statistics. More properly, it is the partitioning of sums of squared deviations or errors. Mathematically, the sum of squared deviations is an unscaled, or unadjusted measure of dispersion...
:
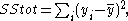the total sum of squaresTotal sum of squares
In statistical data analysis the total sum of squares is a quantity that appears as part of a standard way of presenting results of such analyses...
(proportional to the sample variance);
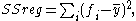the regression sum of squares, also called the explained sum of squaresExplained sum of squares
In statistics, the explained sum of squares is a quantity used in describing how well a model, often a regression model, represents the data being modelled...
.
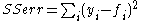, the sum of squares of residuals, also called the residual sum of squaresResidual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
.
In the above
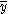is the mean of the observed data: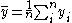where n is the number of observations.
The notations
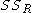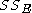and should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.The most general definition of the coefficient of determination is
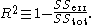
Relation to unexplained variance
In a general form, R2 can be seen to be related to the unexplained variance, since the second term compares the unexplained variance (variance of the model's errors) with the total variance (of the data). See fraction of variance unexplainedFraction of variance unexplained
In statistics, the fraction of variance unexplained in the context of a regression task is the fraction of variance of the regressand Y which cannot be explained, i.e., which is not correctly predicted, by the explanatory variables X....
.
As explained variance
In some cases the total sum of squaresTotal sum of squares
In statistical data analysis the total sum of squares is a quantity that appears as part of a standard way of presenting results of such analyses...
equals the sum of the two other sums of squares defined above,
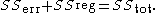
See sum of squares
Sum of squares
The partition of sums of squares is a concept that permeates much of inferential statistics and descriptive statistics. More properly, it is the partitioning of sums of squared deviations or errors. Mathematically, the sum of squared deviations is an unscaled, or unadjusted measure of dispersion...
for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of R2 is equivalent to
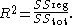
In this form R2 is given directly in terms of the explained variance: it compares the explained variance (variance of the model's predictions) with the total variance (of the data).
This partition of the sum of squares holds for instance when the model values ƒi have been obtained by linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
. A milder sufficient condition reads as follows: The model has the form
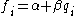
where the qi are arbitrary values that may or may not depend on i or on other free parameters (the common choice qi = xi is just one special case), and the coefficients α and β are obtained by minimizing the residual sum of squares.
This set of conditions is an important one and it has a number of implications for the properties of the fitted residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
and the modelled values. In particular, under these conditions:
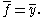
As squared correlation coefficient
Similarly, after least squares regression with a constant+linear model (i.e., simple linear regressionSimple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
), R2 equals the square of the correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between the observed and modeled (predicted) data values.
Under general conditions, an R2 value is sometimes calculated as the square of the correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between the original and modeled data values. In this case, the value is not directly a measure of how good the modeled values are, but rather a measure of how good a predictor might be constructed from the modeled values (by creating a revised predictor of the form α + βƒi). According to Everitt (2002, p. 78), this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables.
Interpretation
R2 is a statistic that will give some information about the goodness of fitGoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
of a model. In regression, the R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1.0 indicates that the regression line perfectly fits the data.
Values of R2 outside the range 0 to 1 can occur where it is used to measure the agreement between observed and modelled values and where the "modelled" values are not obtained by linear regression and depending on which formulation of R2 is used. If the first formula above is used, values can never be greater than one. If the second expression is used, there are no constraints on the values obtainable.
In many (but not all) instances where R2 is used, the predictors are calculated by ordinary least-squares regression: that is, by minimizing SSerr. In this case R-squared increases as we increase the number of variables in the model (R2 will not decrease). This illustrates a drawback to one possible use of R2, where one might try to include more variables in the model until "there is no more improvement". This leads to the alternative approach of looking at the adjusted R2. The explanation of this statistic is almost the same as R2 but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the R2 statistic can be calculated as above and may still be a useful measure. If fitting is by weighted least squares or generalized least squares
Generalized least squares
In statistics, generalized least squares is a technique for estimating the unknown parameters in a linear regression model. The GLS is applied when the variances of the observations are unequal , or when there is a certain degree of correlation between the observations...
, alternative versions of R2 can be calculated appropriate to those statistical frameworks, while the "raw" R2 may still be useful if it is more easily interpreted. Values for R2 can be calculated for any type of predictive model, which need not have a statistical basis.
In a linear model
Consider a linear model of the form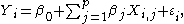where, for the ith case,
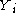is the response variable, 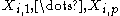are p regressors, and 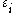is a mean zero errorErrors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
term. The quantities
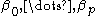are unknown coefficients, whose values are determined by least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
. The coefficient of determination R2 is a measure of the global fit of the model. Specifically, R2 is an element of [0, 1] and represents the proportion of variability in Yi that may be attributed to some linear combination of the regressors (explanatory variables) in X.
R2 is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, R2 = 1 indicates that the fitted model explains all variability in
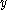, while R2 = 0 indicates no 'linear' relationship (for straight line regression, this means that the straight line model is a constant line (slope=0, intercept=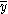) between the response variable and regressors). An interior value such as R2 = 0.7 may be interpreted as follows: "Approximately seventy percent of the variation in the response variable can be explained by the explanatory variable. The remaining thirty percent can be explained by unknown, lurking variableLurking variable
In statistics, a confounding variable is an extraneous variable in a statistical model that correlates with both the dependent variable and the independent variable...
s or inherent variability."
A caution that applies to R2, as to other statistical descriptions of correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
and association is that "correlation does not imply causation
Correlation does not imply causation
"Correlation does not imply causation" is a phrase used in science and statistics to emphasize that correlation between two variables does not automatically imply that one causes the other "Correlation does not imply causation" (related to "ignoring a common cause" and questionable cause) is a...
." In other words, while correlations may provide valuable clues regarding causal relationships among variables, a high correlation between two variables does not represent adequate evidence that changing one variable has resulted, or may result, from changes of other variables.
In case of a single regressor, fitted by least squares, R2 is the square of the Pearson product-moment correlation coefficient
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
relating the regressor and the response variable. More generally, R2 is the square of the correlation between the constructed predictor and the response variable.
Inflation of R2
In least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
regression, R2 is weakly increasing in the number of regressors in the model. As such, R2 alone cannot be used as a meaningful comparison of models with different numbers of independent variables. For a meaningful comparison between two models, an F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
can be performed on the residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
, similar to the F-tests in Granger causality
Granger causality
The Granger causality test is a statistical hypothesis test for determining whether one time series is useful in forecasting another. Ordinarily, regressions reflect "mere" correlations, but Clive Granger, who won a Nobel Prize in Economics, argued that there is an interpretation of a set of tests...
. As a reminder of this, some authors denote R2 by R2p, where p is the number of columns in X
To demonstrate this property, first recall that the objective of least squares regression is:
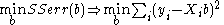
The optimal value of the objective is weakly smaller as additional columns of
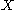are added, by the fact that relatively unconstrained minimization leads to a solution which is weakly smaller than relatively constrained minimization. Given the previous conclusion and noting that 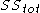depends only on y, the non-decreasing property of R2 follows directly from the definition above.The intuitive reason that using an additional explanatory variable cannot lower the R2 is this: Minimizing
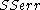is equivalent to maximizing R2. When the extra variable is included, the data always have the option of giving it an estimated coefficient of zero, leaving the predicted values and the R2 unchanged. The only way that the optimization problem will give a non-zero coefficient is if doing so improves the R2.Adjusted R2
Adjusted R2 (often written as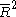 and pronounced "R bar squared") is a modification due to Theil of R2 that adjusts for the number of explanatory terms in a model. Unlike R2, the adjusted R2 increases only if the new term improves the model more than would be expected by chance. The adjusted R2 can be negative, and will always be less than or equal to R2. The adjusted R2 is defined as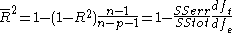where p is the total number of regressors in the linear model (but not counting the constant term), n is the sample size, dft is the degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
n– 1 of the estimate of the population variance of the dependent variable, and dfe is the degrees of freedom n – p – 1 of the estimate of the underlying population error variance.
The principle behind the Adjusted R2 statistic can be seen by rewriting the ordinary R2 as
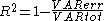
where
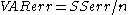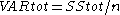and are estimates of the variances of the errors and of the observations, respectively. These estimates are replaced by statistically unbiased versions: 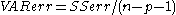and 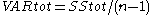.Adjusted R2 does not have the same interpretation as R2. As such, care must be taken in interpreting and reporting this statistic. Adjusted R2 is particularly useful in the Feature selection
Feature selection
In machine learning and statistics, feature selection, also known as variable selection, feature reduction, attribute selection or variable subset selection, is the technique of selecting a subset of relevant features for building robust learning models...
stage of model building..
The use of an adjusted R2 is an attempt to take account of the phenomenon of statistical shrinkage
Shrinkage (statistics)
In statistics, shrinkage has two meanings:*In relation to the general observation that, in regression analysis, a fitted relationship appears to perform less well on a new data set than on the data set used for fitting. In particular the value of the coefficient of determination 'shrinks'...
.
Generalized R2
Nagelkerke (1991) generalizes the definition of the coefficient of determination:- A generalized coefficient of determination should be consistent with the classical coefficient of determination when both can be computed;
- Its value should also be maximised by the maximum likelihood estimation of a model;
- It should be, at least asymptotically, independent of the sample size;
- Its interpretation should be the proportion of the variation explained by the model;
- It should be between 0 and 1, with 0 denoting that model does not explain any variation and 1 denoting that it perfectly explains the observed variation;
- It should not have any unit.
The generalized R² has all of these properties.
where L(0) is the likelihood of the model with only the intercept,
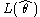is the likelihood of the estimated model and n is the sample size.However, in the case of a logistic model, where
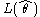cannot be greater than 1, R² is between 0 and 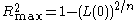: thus, it is possible to define a scaled R² as R²/R²max.See also
- Goodness of fitGoodness of fitThe goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g...
- Fraction of variance unexplainedFraction of variance unexplainedIn statistics, the fraction of variance unexplained in the context of a regression task is the fraction of variance of the regressand Y which cannot be explained, i.e., which is not correctly predicted, by the explanatory variables X....
- Pearson product-moment correlation coefficientPearson product-moment correlation coefficientIn statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
- Nash–Sutcliffe model efficiency coefficient (hydrological applicationsHydrologyHydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
) - Regression model validation
- Proportional reduction in lossProportional reduction in lossProportional reduction in loss refers to a general framework for developing and evaluating measures of the reliability of particular ways of making observations which are possibly subject to errors of all types...
- Root mean square deviationRoot mean square deviationThe root-mean-square deviation is the measure of the average distance between the atoms of superimposed proteins...
- Multiple correlationMultiple correlationIn statistics, multiple correlation is a linear relationship among more than two variables. It is measured by the coefficient of multiple determination, denoted as R2, which is a measure of the fit of a linear regression...