
Sum of squares
Encyclopedia
The partition of sums of squares is a concept that permeates much of inferential statistics and descriptive statistics
. More properly, it is the partitioning of sums of squared deviations
or errors. Mathematically, the sum of squared deviations is an unscaled, or unadjusted measure of dispersion
(also called variability). When scaled for the number of degrees of freedom
, it estimates the variance
, or spread of the observations about their mean value. Partitioning of the sum of squared deviations into various components allows the overall variability in a dataset to be ascribed to different types or sources of variability, with the relative importance of each being quantified by the size of each component of the overall sum of squares.
 , where
, where  is the ith data point, and
is the ith data point, and  is the estimate of the mean. If all such deviations are squared, then summed, as in
is the estimate of the mean. If all such deviations are squared, then summed, as in  including a constant based on a sample
including a constant based on a sample 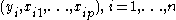 containing n observations, the total sum of squares
containing n observations, the total sum of squares  (TSS) can be partitioned as follows into the explained sum of squares
(TSS) can be partitioned as follows into the explained sum of squares
(ESS) and the residual sum of squares
(RSS):
where this equation is equivalent to each of the following forms:
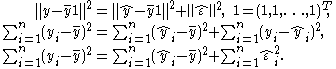
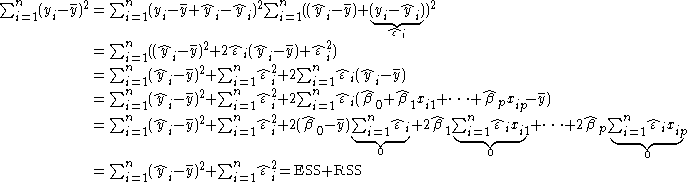
The requirement that the model includes a constant or equivalently that the design matrix contains a column of ones ensures that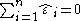 .
.
Some readers may find the following version of the proof, set in vector form, more enlightening:
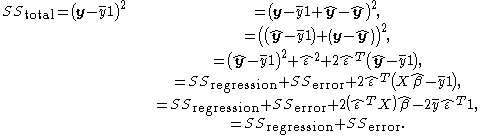
The elimination of terms in the last line, used the fact that
Descriptive statistics
Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
. More properly, it is the partitioning of sums of squared deviations
Squared deviations
In probability theory and statistics, the definition of variance is either the expected value , or average value , of squared deviations from the mean. Computations for analysis of variance involve the partitioning of a sum of squared deviations...
or errors. Mathematically, the sum of squared deviations is an unscaled, or unadjusted measure of dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
(also called variability). When scaled for the number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
, it estimates the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, or spread of the observations about their mean value. Partitioning of the sum of squared deviations into various components allows the overall variability in a dataset to be ascribed to different types or sources of variability, with the relative importance of each being quantified by the size of each component of the overall sum of squares.
Background
The distance from any point in a collection of data, to the mean of the data, is the deviation. This can be written as , where
, where  is the ith data point, and
is the ith data point, and  is the estimate of the mean. If all such deviations are squared, then summed, as in
is the estimate of the mean. If all such deviations are squared, then summed, as in  including a constant based on a sample
including a constant based on a sample 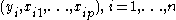 containing n observations, the total sum of squares
containing n observations, the total sum of squares  (TSS) can be partitioned as follows into the explained sum of squares
(TSS) can be partitioned as follows into the explained sum of squaresExplained sum of squares
In statistics, the explained sum of squares is a quantity used in describing how well a model, often a regression model, represents the data being modelled...
(ESS) and the residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
(RSS):

where this equation is equivalent to each of the following forms:
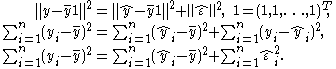
Proof
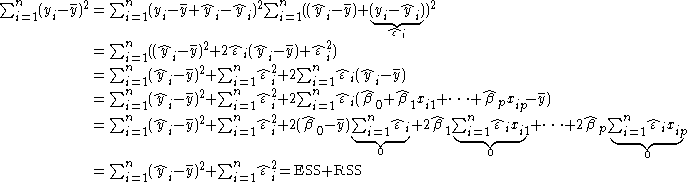
The requirement that the model includes a constant or equivalently that the design matrix contains a column of ones ensures that
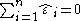 .
.Some readers may find the following version of the proof, set in vector form, more enlightening:
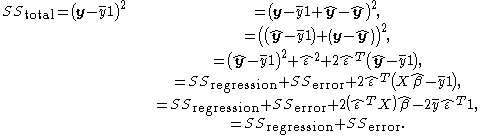
The elimination of terms in the last line, used the fact that
-
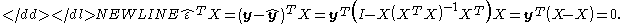
Further partitioning
Note that the residual sum of squares can be further partitioned as the lack-of-fit sum of squaresLack-of-fit sum of squaresIn statistics, a sum of squares due to lack of fit, or more tersely a lack-of-fit sum of squares, is one of the components of a partition of the sum of squares in an analysis of variance, used in the numerator in an F-test of the null hypothesis that says that a proposed model fits well.- Sketch of...
plus the sum of squares due to pure error.
See also
- Inner-product space
- Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
- Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
- Euclidean space
- OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
- Orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
- Orthogonal complement, the closed subspace orthogonal to a set (especially a subspace)
- Orthomodular lattice of the subspaces of an inner-product space
- Orthogonal projection
- Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
that the sum of the squared norms of orthogonal summands equals the squared norm of the sum.
- Hilbert space
- Least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
- Mean squared errorMean squared errorIn statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
- Squared deviationsSquared deviationsIn probability theory and statistics, the definition of variance is either the expected value , or average value , of squared deviations from the mean. Computations for analysis of variance involve the partitioning of a sum of squared deviations...
- Inner-product space

