Feature selection
Encyclopedia
In machine learning
and statistics
, feature selection, also known as variable selection, feature reduction, attribute selection or variable subset selection, is the technique of selecting a subset of relevant features for building robust learning models. When applied in biology
domain, the technique is also called discriminative gene selection, which detects influential genes
based on DNA microarray
experiments. By removing most irrelevant and redundant features from the data, feature selection helps improve the performance of learning models by:
Feature selection also helps people to acquire better understanding about their data by telling them which are the important features and how they are related with each other.
problems requires an exhaustive search of all possible subsets of features of the chosen cardinality. If large numbers of features are available, this is impractical. For practical supervised learning algorithms, the search is for a satisfactory set of features instead of an optimal set.
Feature selection algorithms typically fall into two categories: feature ranking and subset selection. Feature ranking ranks the features by a metric and eliminates all features that do not achieve an adequate score. Subset selection searches the set of possible features for the optimal subset.
In statistics, the most popular form of feature selection is stepwise regression
. It is a greedy algorithm that adds the best feature (or deletes the worst feature) at each round. The main control issue is deciding when to stop the algorithm. In machine learning, this is typically done by cross-validation. In statistics, some criteria are optimized. This leads to the inherent problem of nesting. More robust methods have been explored, such as branch and bound
and piecewise linear network.
Many popular search approaches use greedy
hill climbing
, which iteratively evaluates a candidate subset of features, then modifies the subset and evaluates if the new subset is an improvement over the old. Evaluation of the subsets requires a scoring metric
that grades a subset of features. Exhaustive search is generally impractical, so at some implementor (or operator) defined stopping point, the subset of features with the highest score discovered up to that point is selected as the satisfactory feature subset. The stopping criterion varies by algorithm; possible criteria include: a subset score exceeds a threshold, a program's maximum allowed run time has been surpassed, etc.
Alternative search-based techniques are based on targeted projection pursuit
which finds low-dimensional projections of the data that score highly: the features that have the largest projections in the lower dimensional space are then selected.
Search approaches include:
Two popular filter metrics for classification problems are correlation
and mutual information
, although neither are true metrics
or 'distance measures' in the mathematical sense, since they fail to obey the triangle inequality
and thus do not compute any actual 'distance' – they should rather be regarded as 'scores'. These scores are computed between a candidate feature (or set of features) and the desired output category.
Other available filter metrics include:
statistic and Akaike information criterion
(AIC). These add variables if the t-statistic
is bigger than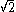
.
Other criteria are Bayesian information criterion (BIC) which uses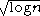
, minimum description length
(MDL) which asymptotically uses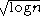
, Bonnferroni / RIC which use 
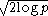, maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rate
(FDR) which use something close to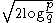
.
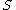for the class 
is defined by the average value of all mutual information values between the individual feature 
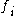and the class 
as follows:
.
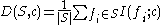The redundancy of all features in the set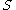
is the average value of all mutual information values between the feature 
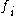and the feature 
:
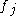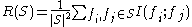
The mRMR criterion is a combination of two measures given above and is defined as follows:
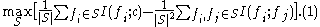
Suppose that there are
full-set features. The binary values of the variable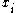 
are used in order to indicate the appearance (
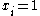) or the absence (
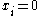) of the feature 
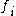in the globally optimal feature set. The mutual information values 
, 
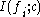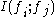are denoted by constants 
, 
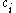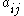, respectively. Therefore, the problem (3) can be described as an optimization problem as follows:
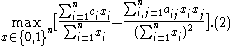
Peng et al. shows that mRMR feature selection is an approximation of the theoretically optimal maximum-dependency feature selection that maximizes the mutual information between the joint distribution of the selected features and the classification variable. However, since mRMR turned a combinatorial problem as a series of much smaller scale problems, each of which only involves two variables, the estimation of joint probabilities is much more robust. Overall the algorithm is much more efficient than the theoretically optimal max-dependency selection, while it is more robust to find useful features.
It can be seen that mRMR is also related to the correlation based feature selection below. It may also be seen a special case of some generic feature selectors .
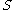consisting of 
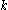features:
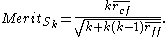
Here,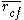
is the average value of all feature-classification correlations, and 
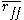is the average value of all feature-feature correlations. The CFS criterion is defined as follows:
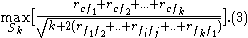
By using binary values of the variable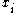
as in the case of the mRMR measure to indicate the appearance or the absence of the feature 
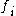, the problem (4) can be rewritten as an optimization problem as follows:
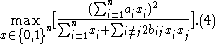
Combinatorial problems (2) and (4) are, in fact, mixed 0-1 linear programming problems that can be solved by using branch-and-bound algorithms .
, NumPy and the R language
. Other software systems are tailored specifically to the feature-selection task:
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, feature selection, also known as variable selection, feature reduction, attribute selection or variable subset selection, is the technique of selecting a subset of relevant features for building robust learning models. When applied in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
domain, the technique is also called discriminative gene selection, which detects influential genes
Gênes
Gênes is the name of a département of the First French Empire in present Italy, named after the city of Genoa. It was formed in 1805, when Napoleon Bonaparte occupied the Republic of Genoa. Its capital was Genoa, and it was divided in the arrondissements of Genoa, Bobbio, Novi Ligure, Tortona and...
based on DNA microarray
DNA microarray
A DNA microarray is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome...
experiments. By removing most irrelevant and redundant features from the data, feature selection helps improve the performance of learning models by:
- Alleviating the effect of the curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
. - Enhancing generalization capability.
- Speeding up learning process.
- Improving model interpretability.
Feature selection also helps people to acquire better understanding about their data by telling them which are the important features and how they are related with each other.
Introduction
Simple feature selection algorithms are ad hoc, but there are also more methodical approaches. From a theoretical perspective, it can be shown that optimal feature selection for supervised learningSupervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
problems requires an exhaustive search of all possible subsets of features of the chosen cardinality. If large numbers of features are available, this is impractical. For practical supervised learning algorithms, the search is for a satisfactory set of features instead of an optimal set.
Feature selection algorithms typically fall into two categories: feature ranking and subset selection. Feature ranking ranks the features by a metric and eliminates all features that do not achieve an adequate score. Subset selection searches the set of possible features for the optimal subset.
In statistics, the most popular form of feature selection is stepwise regression
Stepwise regression
In statistics, stepwise regression includes regression models in which the choice of predictive variables is carried out by an automatic procedure...
. It is a greedy algorithm that adds the best feature (or deletes the worst feature) at each round. The main control issue is deciding when to stop the algorithm. In machine learning, this is typically done by cross-validation. In statistics, some criteria are optimized. This leads to the inherent problem of nesting. More robust methods have been explored, such as branch and bound
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
and piecewise linear network.
Subset selection
Subset selection evaluates a subset of features as a group for suitability. Subset selection algorithms can be broken into Wrappers, Filters and Embedded. Wrappers use a search algorithm to search through the space of possible features and evaluate each subset by running a model on the subset. Wrappers can be computationally expensive and have a risk of over fitting to the model. Filters are similar to Wrappers in the search approach, but instead of evaluating against a model, a simpler filter is evaluated. Embedded techniques are embedded in and specific to a model.Many popular search approaches use greedy
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
hill climbing
Hill climbing
In computer science, hill climbing is a mathematical optimization technique which belongs to the family of local search. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by incrementally changing a single element of the solution...
, which iteratively evaluates a candidate subset of features, then modifies the subset and evaluates if the new subset is an improvement over the old. Evaluation of the subsets requires a scoring metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
that grades a subset of features. Exhaustive search is generally impractical, so at some implementor (or operator) defined stopping point, the subset of features with the highest score discovered up to that point is selected as the satisfactory feature subset. The stopping criterion varies by algorithm; possible criteria include: a subset score exceeds a threshold, a program's maximum allowed run time has been surpassed, etc.
Alternative search-based techniques are based on targeted projection pursuit
Targeted projection pursuit
Targeted projection pursuit is a type of statistical technique used for exploratory data analysis, information visualization, and feature selection...
which finds low-dimensional projections of the data that score highly: the features that have the largest projections in the lower dimensional space are then selected.
Search approaches include:
- Exhaustive
- Best first
- Simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
- Genetic algorithmGenetic algorithmA genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
- GreedyGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
forward selection - GreedyGreedy algorithmA greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
backward elimination - Targeted projection pursuitTargeted projection pursuitTargeted projection pursuit is a type of statistical technique used for exploratory data analysis, information visualization, and feature selection...
Two popular filter metrics for classification problems are correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
and mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, although neither are true metrics
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
or 'distance measures' in the mathematical sense, since they fail to obey the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
and thus do not compute any actual 'distance' – they should rather be regarded as 'scores'. These scores are computed between a candidate feature (or set of features) and the desired output category.
Other available filter metrics include:
- Class separability
- Error probability
- Inter-class distance
- Probabilistic distance
- Entropy
- Consistency-based feature selection
- Correlation-based feature selection
Optimality criteria
There are a variety of optimality criteria that can be used for controlling feature selection. The oldest are Mallows' CpMallows' Cp
In statistics, Mallows' Cp, named for Colin L. Mallows, is used to assess the fit of a regression model that has been estimated using ordinary least squares. It is applied in the context of model selection, where a number of predictor variables are available for predicting some outcome, and the...
statistic and Akaike information criterion
Akaike information criterion
The Akaike information criterion is a measure of the relative goodness of fit of a statistical model. It was developed by Hirotsugu Akaike, under the name of "an information criterion" , and was first published by Akaike in 1974...
(AIC). These add variables if the t-statistic
Student's t-test
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
is bigger than
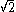.Other criteria are Bayesian information criterion (BIC) which uses
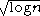, minimum description lengthMinimum description length
The minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
(MDL) which asymptotically uses
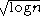, Bonnferroni / RIC which use 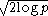, maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rateFalse discovery rate
False discovery rate control is a statistical method used in multiple hypothesis testing to correct for multiple comparisons. In a list of rejected hypotheses, FDR controls the expected proportion of incorrectly rejected null hypotheses...
(FDR) which use something close to
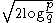.Minimum-redundancy-maximum-relevance (mRMR) feature selection
Peng et al. proposed an mRMR feature-selection method that can use either mutual information, correlation, distance/similarity scores to select features. For example, with mutual information, relevant features and redundant features are considered simultaneously. 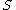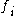The relevance of a feature set for the class is defined by the average value of all mutual information values between the individual feature and the class as follows: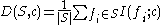.The redundancy of all features in the set
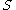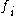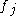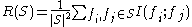
is the average value of all mutual information values between the feature and the feature :The mRMR criterion is a combination of two measures given above and is defined as follows:
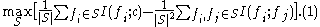
Suppose that there are
full-set features. The binary values of the variable 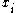are used in order to indicate the appearance (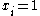) or the absence (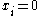) of the feature 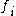in the globally optimal feature set. The mutual information values 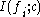, 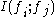are denoted by constants 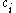, , 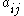respectively. Therefore, the problem (3) can be described as an optimization problem as follows: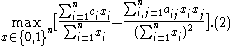Peng et al. shows that mRMR feature selection is an approximation of the theoretically optimal maximum-dependency feature selection that maximizes the mutual information between the joint distribution of the selected features and the classification variable. However, since mRMR turned a combinatorial problem as a series of much smaller scale problems, each of which only involves two variables, the estimation of joint probabilities is much more robust. Overall the algorithm is much more efficient than the theoretically optimal max-dependency selection, while it is more robust to find useful features.
It can be seen that mRMR is also related to the correlation based feature selection below. It may also be seen a special case of some generic feature selectors .
Correlation feature selection
The Correlation Feature Selection (CFS) measure evaluates subsets of features on the basis of the following hypothesis: "Good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other" . The following equation gives the merit of a feature subset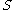 consisting of features:Here,
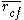is the average value of all feature-classification correlations, and 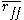is the average value of all feature-feature correlations. The CFS criterion is defined as follows: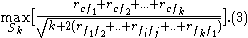By using binary values of the variable
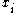as in the case of the mRMR measure to indicate the appearance or the absence of the feature 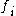, the problem (4) can be rewritten as an optimization problem as follows: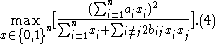Combinatorial problems (2) and (4) are, in fact, mixed 0-1 linear programming problems that can be solved by using branch-and-bound algorithms .
Embedded methods incorporating feature selection
- Random multinomial logitRandom multinomial logitIn statistics and machine learning, random multinomial logit is a technique for statistical classification using repeated multinomial logit analyses via Leo Breiman's random forests.-Rationale for the new method:...
(RMNL) - Sparse regression, LASSO
- Regularized trees e.g. regularized random forest implemented in the RRF package
- Decision treeDecision tree learningDecision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
- Memetic algorithmMemetic algorithmMemetic algorithms represent one of the recent growing areas of research in evolutionary computation. The term MA is now widely used as a synergy of evolutionary or any population-based approach with separate individual learning or local improvement procedures for problem search...
- Auto-encoding networks with a bottleneck-layer
- Many other machine learningMachine learningMachine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
methods applying a pruningPruning (algorithm)Pruning is a technique in machine learning that reduces the size of decision trees by removing sections of the tree that provide little power to classify instances...
step.
Software for feature selection
Many standard data analysis software systems are often used for feature selection, such as SciLabScilab
Scilab is an open source, cross-platform numerical computational package and a high-level, numerically oriented programming language. Itcan be used for signal processing, statistical analysis, image enhancement, fluid dynamics simulations, numerical optimization, and modeling and simulation of...
, NumPy and the R language
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
. Other software systems are tailored specifically to the feature-selection task:
- WekaWeka (machine learning)Weka is a popular suite of machine learning software written in Java, developed at the University of Waikato, New Zealand...
– freely available and open-sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
software in Java. - Feature Selection Toolbox 3Feature Selection ToolboxFeature Selection Toolbox is a machine learning software focusing primarily on the feature selection problem, written in C++, developed at the Institute of Information Theory and Automation , of the Czech Academy of Sciences....
– freely available and open-sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
software in C++. - RapidMiner – freely available and open-sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
software. - OrangeOrange (software)Orange is a component-based data mining and machine learning software suite, featuring friendly yet powerful and flexible visual programming front-end for explorative data analysis and visualization, and Python bindings and libraries for scripting...
– freely available and open-sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
software (module orngFSS). - TOOLDIAG Pattern recognition toolbox – freely available C toolbox.
- minimum redundancy feature selection tool – freely available C/Matlab codes for selecting minimum redundant features.
- A C# Implementation of greedy forward feature subset selection for various classifiers (e.g., LibLinear, SVM-light).
- MCFS-ID (Monte Carlo Feature Selection and Interdependency Discovery) is a Monte Carlo method-based tool for feature selection. It also allows for the discovery of interdependencies between the relevant features. MCFS-ID is particularly suitable for the analysis of high-dimensional, ill-defined transactional and biological data.
- RRF is a relatively new R package for feature selection and can be installed from R. RRF stands for Regularized Random Forest, which is a type of Regularized Trees. By building a regularized random forest, a compact set of non-redundant features can be selected without loss of predictive information. Regularized trees can capture non-linear interactions between variables, and naturally handle different scales, and numerical and categorical variables.
See also
- Cluster analysis
- Dimensionality reductionDimensionality reductionIn machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...
- Feature extractionFeature extractionIn pattern recognition and in image processing, feature extraction is a special form of dimensionality reduction.When the input data to an algorithm is too large to be processed and it is suspected to be notoriously redundant then the input data will be transformed into a reduced representation...
- Data miningData miningData mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
Further reading
- Tutorial Outlining Feature Selection Algorithms
- JMLR Special Issue on Variable and Feature Selection
- Deng, H; Runger, G; Tuv, Eugene (2011). Bias of importance measures for multi-valued attributes and solutions, Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN2011). pp. 293-300
- Feature Selection for Knowledge Discovery and Data Mining (Book)
- An Introduction to Variable and Feature Selection (Survey)
- Toward integrating feature selection algorithms for classification and clustering (Survey)
- Efficient Feature Subset Selection and Subset Size Optimization (Survey, 2010)
- Searching for Interacting Features
- Feature Subset Selection Bias for Classification Learning
- Y. Sun, S. Todorovic, S. Goodison, Local Learning Based Feature Selection for High-dimensional Data Analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 32, no. 9, pp. 1610-1626, 2010.
External links
- NIPS challenge 2003 (see also NIPS)
- Naive Bayes implementation with feature selection in Visual Basic (includes executable and source code)
- Minimum-redundancy-maximum-relevance (mRMR) feature selection program