False discovery rate
Encyclopedia
False discovery rate control is a statistical
method used in multiple hypothesis testing to correct for multiple comparisons
. In a list of rejected hypotheses, FDR controls the expected
proportion of incorrectly rejected null hypotheses
(type I
errors). It is a less conservative procedure for comparison, with greater power than familywise error rate
(FWER) control, at a cost of increasing the likelihood of obtaining type I
errors.
In practical terms, the FDR is the expected proportion of false positives among all significant hypotheses; for example, if 1000 observations were experimentally predicted to be different, and a maximum FDR for these observations was 0.10, then 100 of these observations would be expected to be false positives.
The q-value is defined to be the FDR analogue of the p-value
. The q-value of an individual hypothesis test is the minimum FDR at which the test may be called significant. One approach is to directly estimate q-values rather than fixing a level at which to control the FDR.
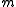hypothesis tests.
The false discovery rate is given by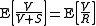
and one wants to keep this value below a threshold 
.
(
is defined to be 0 when 
)
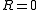on a given data set. In this environment, traditional multiple comparison procedures
began to appear as too conservative. The False Discovery Rate concept was formally described by Benjamini and Hochberg (1995) as a less conservative and arguably more appropriate approach for identifying the important few from the trivial many effects tested. Efron and others have since connected it to the literature on
Empirical Bayes
..
Users of statistical testing procedures care more about whether a particular effect identified as real by a test actually is real than they do about the probability that it was so identified if it were not real, the p-value
. However, the p-value was generally the closest available concept for judging whether an effect was real prior to recent developments in the theory and methods for FDR computation.
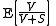is less than a given 
. This procedure is valid when the 
tests are independent
. Let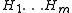
be the null hypotheses and 
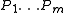their corresponding p-value
s. Order these values in increasing order and denote them by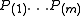
. For a given 
, find the largest 
such that 
Then reject (i.e. declare positive) all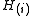
for 
.
Note that the mean
for these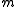 
tests is 
which could be used as a rough FDR, or RFDR, "
adjusted for 
independent (or positively correlated, see below) tests." The RFDR calculation shown here provides a useful approximation and is not part of the Benjamini and Hochberg method; see AFDR below.
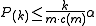
In the case of negative correlation,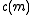
can be approximated by using the Euler–Mascheroni constant
.
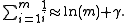
Using RFDR above, an approximate FDR, or AFDR, is the min(mean α) for m tests = RFDR / ( ln(m) + 0.57721...).
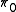be the probability that the null hypothesis is correct, and 
be the probability that the alternative is correct. Then 
times the average p-value of rejected effects divided by the number of rejected effects gives an estimate of the FDR. While we do not know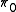 
, it is typically close enough to 1 that we can get a reasonable estimate of the FDR by assuming it is 1. This and many related results are discussed in Efron (2010).
| doi = 10.1111/1467-9868.00346}}
| doi = 10.1214/aos/1074290335
| url = http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.aos/1074290335}}
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
method used in multiple hypothesis testing to correct for multiple comparisons
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
. In a list of rejected hypotheses, FDR controls the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
proportion of incorrectly rejected null hypotheses
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
(type I
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
errors). It is a less conservative procedure for comparison, with greater power than familywise error rate
Familywise error rate
In statistics, familywise error rate is the probability of making one or more false discoveries, or type I errors among all the hypotheses when performing multiple pairwise tests.-Classification of m hypothesis tests:...
(FWER) control, at a cost of increasing the likelihood of obtaining type I
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
errors.
In practical terms, the FDR is the expected proportion of false positives among all significant hypotheses; for example, if 1000 observations were experimentally predicted to be different, and a maximum FDR for these observations was 0.10, then 100 of these observations would be expected to be false positives.
The q-value is defined to be the FDR analogue of the p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
. The q-value of an individual hypothesis test is the minimum FDR at which the test may be called significant. One approach is to directly estimate q-values rather than fixing a level at which to control the FDR.
Classification of m hypothesis tests
The following table defines some random variables related to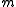 hypothesis tests.
| Null hypothesis is True (H0) | Alternative hypothesis is True (H1) | Total | |
|---|---|---|---|
| Declared significant |  |
 |
 |
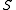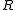| Declared non-significant |  |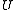
 |
 |
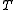| Total |  |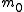
 |
 |
-
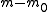is the total number hypotheses tested -
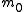is the number of true null hypothesesNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position... -
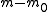is the number of true alternative hypotheses -
is the number of false positives (Type I error)Type I and type II errorsIn statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or... -
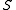is the number of true positivesType I and type II errorsIn statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or... -
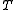is the number of false negatives (Type II error)Type I and type II errorsIn statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or... -
is the number of true negativesType I and type II errorsIn statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
- In
hypothesis tests of which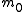 
are true null hypotheses, 
is an observable random variable, 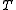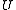and 
, 
, 
, and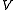 
are unobservable random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
The false discovery rate is given by
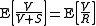and one wants to keep this value below a threshold .(
is defined to be 0 when 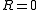)History
By the 1980s and 1990s, advanced technology had made it possible to perform hundreds and thousands of statistical testsStatistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
on a given data set. In this environment, traditional multiple comparison procedures
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
began to appear as too conservative. The False Discovery Rate concept was formally described by Benjamini and Hochberg (1995) as a less conservative and arguably more appropriate approach for identifying the important few from the trivial many effects tested. Efron and others have since connected it to the literature on
Empirical Bayes
Empirical Bayes method
Empirical Bayes methods are procedures for statistical inference in which the prior distribution is estimated from the data. This approach stands in contrast to standardBayesian methods, for which the prior distribution is fixed before any data are observed...
..
Users of statistical testing procedures care more about whether a particular effect identified as real by a test actually is real than they do about the probability that it was so identified if it were not real, the p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
. However, the p-value was generally the closest available concept for judging whether an effect was real prior to recent developments in the theory and methods for FDR computation.
Independent tests
The Simes procedure ensures that its expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
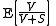is less than a given . This procedure is valid when the tests are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. Let
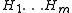be the null hypotheses and 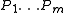their corresponding p-valueP-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
s. Order these values in increasing order and denote them by
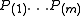. For a given , find the largest such that Then reject (i.e. declare positive) all
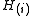for .Note that the mean
for these 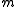tests is which could be used as a rough FDR, or RFDR, " adjusted for independent (or positively correlated, see below) tests." The RFDR calculation shown here provides a useful approximation and is not part of the Benjamini and Hochberg method; see AFDR below.Dependent tests
The Benjamini–Hochberg–Yekutieli procedure controls the false discovery rate under dependence assumptions. This refinement modifies the threshold and finds the largest k such that: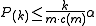- If the tests are independent: c(m) = 1 (same as above)
- If the tests are positively correlated: c(m) = 1
- If the tests are negatively correlated:
In the case of negative correlation,
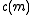can be approximated by using the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
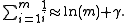
Using RFDR above, an approximate FDR, or AFDR, is the min(mean α) for m tests = RFDR / ( ln(m) + 0.57721...).
Large-Scale Inference
Let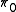 be the probability that the null hypothesis is correct, and be the probability that the alternative is correct. Then times the average p-value of rejected effects divided by the number of rejected effects gives an estimate of the FDR. While we do not know 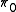, it is typically close enough to 1 that we can get a reasonable estimate of the FDR by assuming it is 1. This and many related results are discussed in Efron (2010).Further Reading
| doi = 10.1214/aos/1013699998}}| doi = 10.1111/1467-9868.00346}}
| doi = 10.1214/aos/1074290335
| url = http://projecteuclid.org/DPubS?service=UI&version=1.0&verb=Display&handle=euclid.aos/1074290335}}
External links
- False Discovery Rate Analysis in R – Lists links with popular RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
packages