
Familywise error rate
Encyclopedia
In statistics
, familywise error rate (FWER) is the probability
of making one or more false discoveries, or type I error
s among all the hypotheses when performing multiple pairwise tests
.
The m specific hypotheses of interest are assumed to be known, but the number of true null hypotheses m0 and of alternative hypotheses m1, are unknown. V is the number of Type I errors
(hypotheses declared significant when they are actually from the null distribution). T is the number of Type II errors
(hypotheses declared not significant when they are actually from the alternative distribution). R is an observable random variable
, while S, T , U, and V are unobservable random variables.
In terms of random variables,
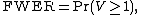
or equivalently,
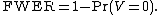
For example, one might conduct a randomized clinical trial for a new antidepressant drug using three groups: existing drug, new drug, and placebo. In such a design, one might be interested in whether depressive symptoms (measured, for example, by a Beck Depression Inventory
score) decreased to a greater extent for those using the new drug compared to the old drug. Further, one might be interested in whether any side effect
s (e.g., hypersomnia
, decreased sex drive, and dry mouth) were observed. In such a case, two families would likely be identified: 1) effect of drug on depressive symptoms, 2) occurrence of any side effects.
Thus, one would assign an acceptable Type I error rate, alpha, (usually 0.05) to each family and control for family-wise error using appropriate multiple comparison procedures. In the case of the first family, effect of antidepressant on depressive symptoms, pairwise comparison
s among groups (here, there would be three possible comparisons) would be jointly controlled using techniques such as Tukey's Honestly Significant Difference (HSD) comparison procedure or a Bonferroni correction
. In terms of the side effect profile, one would likely be interested in controlling for Type I error in terms of all side effects considered jointly so that decisions about the side effect profile would not be erroneously inflated by allowing each side effect and each pairwise comparison among groups to receive its own uncorrected alpha. By the Bonferroni inequality, allowing each side effect and comparison its own alpha would result in a Type I error of 0.05 × 3 side effects × 3 pairwise comparisons per side effect = 0.45 (i.e., 45% chance of making a Type I error). Thus, a more appropriate control for side effect family-wise error might divide alpha by three (0.05/3 = 0.0167) and allocate .0167 to each side effect multiple comparison procedure. In the case of Tukey's HSD (a strong control multiple comparison procedure), one would determine the critical value of Q, the studentized range statistic, based on the alpha of 0.0167.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, familywise error rate (FWER) is the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of making one or more false discoveries, or type I error
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
s among all the hypotheses when performing multiple pairwise tests
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
.
Classification of m hypothesis tests
The following table defines some random variables related to the m hypothesis tests.| # declared non-significant.. | # declared significant | Total | |
|---|---|---|---|
| # true null hypotheses |  |
 |
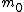 |
| # non-true null hypotheses | 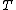 |
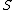 |
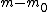 |
| Total |  |
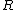 |
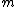 |
The m specific hypotheses of interest are assumed to be known, but the number of true null hypotheses m0 and of alternative hypotheses m1, are unknown. V is the number of Type I errors
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
(hypotheses declared significant when they are actually from the null distribution). T is the number of Type II errors
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
(hypotheses declared not significant when they are actually from the alternative distribution). R is an observable random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, while S, T , U, and V are unobservable random variables.
In terms of random variables,
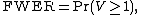
or equivalently,
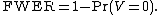
What constitutes a family?
In confirmatory studies (i.e., where one specifies a finite number of a priori inferences), families of hypotheses are defined by which conclusions need to be jointly accurate or by which hypotheses are similar in content/purpose. As noted by Hochberg and Tamhane (1987), "If these inferences are unrelated in terms of their content or intended use (although they may be statistically dependent), then they should be treated separately and not jointly" (p. 6).For example, one might conduct a randomized clinical trial for a new antidepressant drug using three groups: existing drug, new drug, and placebo. In such a design, one might be interested in whether depressive symptoms (measured, for example, by a Beck Depression Inventory
Beck Depression Inventory
The Beck Depression Inventory , created by Dr. Aaron T. Beck, is a 21-question multiple-choice self-report inventory, one of the most widely used instruments for measuring the severity of depression...
score) decreased to a greater extent for those using the new drug compared to the old drug. Further, one might be interested in whether any side effect
Side effect
In medicine, a side effect is an effect, whether therapeutic or adverse, that is secondary to the one intended; although the term is predominantly employed to describe adverse effects, it can also apply to beneficial, but unintended, consequences of the use of a drug.Occasionally, drugs are...
s (e.g., hypersomnia
Hypersomnia
Hypersomnia is a disorder characterized by excessive amounts of sleepiness.There are two main categories of hypersomnia: primary hypersomnia and recurrent hypersomnia...
, decreased sex drive, and dry mouth) were observed. In such a case, two families would likely be identified: 1) effect of drug on depressive symptoms, 2) occurrence of any side effects.
Thus, one would assign an acceptable Type I error rate, alpha, (usually 0.05) to each family and control for family-wise error using appropriate multiple comparison procedures. In the case of the first family, effect of antidepressant on depressive symptoms, pairwise comparison
Pairwise comparison
Pairwise comparison generally refers to any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social...
s among groups (here, there would be three possible comparisons) would be jointly controlled using techniques such as Tukey's Honestly Significant Difference (HSD) comparison procedure or a Bonferroni correction
Bonferroni correction
In statistics, the Bonferroni correction is a method used to counteract the problem of multiple comparisons. It was developed and introduced by Italian mathematician Carlo Emilio Bonferroni...
. In terms of the side effect profile, one would likely be interested in controlling for Type I error in terms of all side effects considered jointly so that decisions about the side effect profile would not be erroneously inflated by allowing each side effect and each pairwise comparison among groups to receive its own uncorrected alpha. By the Bonferroni inequality, allowing each side effect and comparison its own alpha would result in a Type I error of 0.05 × 3 side effects × 3 pairwise comparisons per side effect = 0.45 (i.e., 45% chance of making a Type I error). Thus, a more appropriate control for side effect family-wise error might divide alpha by three (0.05/3 = 0.0167) and allocate .0167 to each side effect multiple comparison procedure. In the case of Tukey's HSD (a strong control multiple comparison procedure), one would determine the critical value of Q, the studentized range statistic, based on the alpha of 0.0167.
See also
- Experimentwise error rateExperimentwise error rateIn statistics, during multiple comparisons testing, experimentwise error rate is the probability of at least one false rejection of the null hypothesis over an entire experiment. The α that is assigned applies to all of the hypothesis tests as a whole, not individually as in the comparisonwise...
- False discovery rateFalse discovery rateFalse discovery rate control is a statistical method used in multiple hypothesis testing to correct for multiple comparisons. In a list of rejected hypotheses, FDR controls the expected proportion of incorrectly rejected null hypotheses...
- Holm-Bonferroni methodHolm-Bonferroni methodIn statistics, the Holm–Bonferroni method performs more than one hypothesis test simultaneously. It is named after Sture Holm and Carlo Emilio Bonferroni.- Procedure :...
- Closed testing procedureClosed testing procedureIn statistics, the closed testing procedure is a general method for performing more than one hypothesis test simultaneously.-The closed testing principle:...
- IncidentalomeIncidentalomeThe incidentalome is the phenomenon of all possible incidental findings.The term was coined as an extension of incidentaloma which refers to the incidental, often radiographic findings of masses or tumors whose significance and prognosis is therefore poorly understood...

