
Generalized least squares
Encyclopedia
In statistics
, generalized least squares (GLS) is a technique for estimating the unknown parameter
s in a linear regression
model. The GLS is applied when the variance
s of the observations are unequal (heteroscedasticity), or when there is a certain degree of correlation
between the observations. In these cases ordinary least squares
can be statistically inefficient
, or even give misleading inferences
.
model we observe data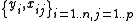 on n statistical units. The response values are placed in a vector Y = (y1, ..., yn)′, and the predictor values are placed in the design matrix X = xij, where xij is the value of the jth predictor variable for the ith unit. The model assumes that the conditional mean of Y given X is a linear function of X, whereas the conditional variance
on n statistical units. The response values are placed in a vector Y = (y1, ..., yn)′, and the predictor values are placed in the design matrix X = xij, where xij is the value of the jth predictor variable for the ith unit. The model assumes that the conditional mean of Y given X is a linear function of X, whereas the conditional variance
of Y given X is a known matrix Ω. This is usually written as
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, generalized least squares (GLS) is a technique for estimating the unknown parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s in a linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
model. The GLS is applied when the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s of the observations are unequal (heteroscedasticity), or when there is a certain degree of correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
between the observations. In these cases ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
can be statistically inefficient
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
, or even give misleading inferences
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
.
Method outline
In a typical linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
model we observe data
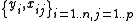 on n statistical units. The response values are placed in a vector Y = (y1, ..., yn)′, and the predictor values are placed in the design matrix X = xij, where xij is the value of the jth predictor variable for the ith unit. The model assumes that the conditional mean of Y given X is a linear function of X, whereas the conditional variance
on n statistical units. The response values are placed in a vector Y = (y1, ..., yn)′, and the predictor values are placed in the design matrix X = xij, where xij is the value of the jth predictor variable for the ith unit. The model assumes that the conditional mean of Y given X is a linear function of X, whereas the conditional varianceCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of Y given X is a known matrix Ω. This is usually written as
-
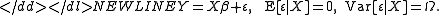
Here β is a vector of unknown “regression coefficients” that must be estimated from the data.
Suppose b is a candidate estimate for β. Then the residualErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
vector for b will be Y − Xb. Generalized least squares method estimates β by minimizing the squared Mahalanobis lengthMahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...
of this residual vector:-
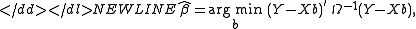
Since the objective is a quadratic form in b, the estimator has an explicit formula:-
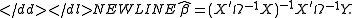
Properties
The GLS estimator is unbiasedBias of an estimatorIn statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
, consistentConsistent estimatorIn statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
, efficientEfficiency (statistics)In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
, and asymptotically normalAsymptotic distributionIn mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
:-

GLS is equivalent to applying ordinary least squares to a linearly transformed version of the data. To see this, factor , for instance using the Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
. Then if we multiply both sides of the equation by B−1, we get an equivalent linear model , where , , and . In this model . Thus we can efficiently estimate β by applying OLS to the transformed data, which requires minimizing-
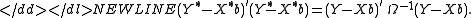
This has the effect of standardizing the scale of the errors and “de-correlating” them. Since OLS is applied to data with homoscedastic errors, the Gauss–Markov theorem applies, and therefore the GLS estimate is the best linear unbiased estimator for β.
Weighted least squares
A special case of GLS called weighted least squares occurs when all the off-diagonal entries of Ω are 0. This situation arises when the variances of the observed values are unequal (i.e. heteroscedasticity is present), but where no correlations exist among the observed values. The weight for unit i is proportional to the reciprocal of the variance of the response for unit i.
Feasible generalized least squares
Feasible generalized least squares is similar to generalized least squares except that it uses an estimated variance-covariance matrix since the true matrix is not known directly.
The ordinary least squaresOrdinary least squaresIn statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
(OLS) estimator is calculated as usual by
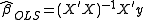
and estimates of the residuals are constructed.
are constructed.
Construct :
:
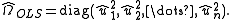
Estimate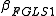 using
using 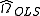 using weighted least squares
using weighted least squares
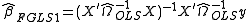
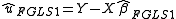
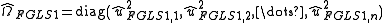

This estimation of can be iterated to convergence given that the assumptions outlined in White hold.
can be iterated to convergence given that the assumptions outlined in White hold.
The WLS and FGLS estimators have the following distributions
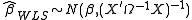
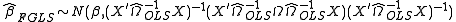
See also
- Iteratively reweighted least squares
- Confidence regionConfidence regionIn statistics, a confidence region is a multi-dimensional generalization of a confidence interval. It is a set of points in an n-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur.The confidence region is...
- Effective degrees of freedom
-
-
-
-

