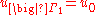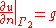Mixed boundary condition
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a mixed boundary condition for a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
indicates that different boundary conditions are used on different parts of the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the equation.
For example, if u is a solution to a partial differential equation on a set
with piecewisePiecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
-smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
boundary
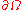, and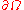 
is divided into two parts, 
and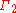 
, one can use a Dirichlet boundary conditionDirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
on
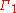and a Neumann boundary conditionNeumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
on
:
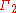where u₀ and g are given functions defined on those portions of the boundary.
Robin boundary condition
Robin boundary condition
In mathematics, the Robin boundary condition is a type of boundary condition, named after Victor Gustave Robin . When imposed on an ordinary or a partial differential equation, it is a specification of a linear combination of the values of a function and the values of its derivative on the...
is another type of hybrid boundary condition; it is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of Dirichlet and Neumann boundary conditions.
See also
- Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
- Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
- Cauchy boundary conditionCauchy boundary conditionIn mathematics, a Cauchy boundary condition imposed on an ordinary differential equation or a partial differential equation specifies both the values a solution of a differential equation is to take on the boundary of the domain and the normal derivative at the boundary. It corresponds to imposing...
- Robin boundary conditionRobin boundary conditionIn mathematics, the Robin boundary condition is a type of boundary condition, named after Victor Gustave Robin . When imposed on an ordinary or a partial differential equation, it is a specification of a linear combination of the values of a function and the values of its derivative on the...