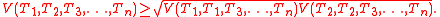Mixed volume
Encyclopedia
In mathematics
, more specifically, in convex geometry
, the mixed volume is a way to associate a non-negative number to an n-tuple of convex bodies
in the n-dimensional space. This number depends on the size of the bodies and their relative positions.
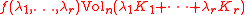
of non-negative λ-s, where Voln stands for the n-dimensional volume. One can show that f is a homogeneous polynomial
of degree n, therefore it can be written as
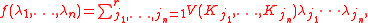
where the functions V are symmetric. Then V(T1, ..., Tn) is called the mixed volume of T1, T2, ..., Tn.
Equivalently,
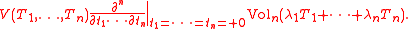
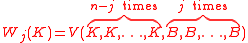
is called the j-th quermassintegral of K.
The definition of mixed volume yields the Steiner formula (named after Jakob Steiner
):
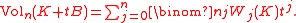

where κn−j is the volume of the (n − j)-dimensional ball.
on convex bodies in Rn that is continuous and invariant under rigid motions of Rn is a linear combination of the quermassintegrals (or, equivalently, of the intrinsic volumes).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically, in convex geometry
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
, the mixed volume is a way to associate a non-negative number to an n-tuple of convex bodies
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
in the n-dimensional space. This number depends on the size of the bodies and their relative positions.
Definition
Let K1, K2, ..., Kr be convex bodies in Rn, and consider the function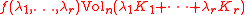
of non-negative λ-s, where Voln stands for the n-dimensional volume. One can show that f is a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree n, therefore it can be written as
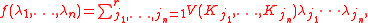
where the functions V are symmetric. Then V(T1, ..., Tn) is called the mixed volume of T1, T2, ..., Tn.
Equivalently,
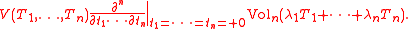
Properties
- The mixed volume is uniquely determined by the following three properties:
- V(T, ...., T) = Voln(T);
- V is symmetric in its arguments;
- V is multilinear: V(a T + b S, T2, ..., Tn) =a V(T, T2, ..., Tn) + b V(S, T2, ..., Tn) for a,b ≥ 0.
- The mixed volume is non-negative, and increasing in each variable.
- The Alexandrov–Fenchel inequality, discovered by Aleksandr Danilovich AleksandrovAleksandr Danilovich AleksandrovAleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
and Werner FenchelWerner FenchelMoritz Werner Fenchel was a mathematician known for his contributions to geometry and to optimization theory. Fenchel established the basic results of convex analysis and nonlinear optimization theory. Fenchel's monographs and lecture-notes were very influential also...
:
- Numerous geometric inequalities, such as the Brunn–Minkowski inequality for convex bodies and Minkowski's first inequalityMinkowski's first inequality for convex bodiesIn mathematics, Minkowski's first inequality for convex bodies is a geometrical result due to the German mathematician Hermann Minkowski. The inequality is closely related to the Brunn–Minkowski inequality and the isoperimetric inequality....
, are special cases of the Alexandrov–Fenchel inequality.
Quermassintegrals
Let K ⊂ Rn be a convex body, and let B ⊂ Rn be the Euclidean ball. The mixed volume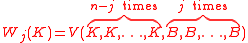
is called the j-th quermassintegral of K.
The definition of mixed volume yields the Steiner formula (named after Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
):
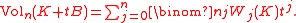
Intrinsic volumes
The j-th intrinsic volume of K is defined by
where κn−j is the volume of the (n − j)-dimensional ball.
Hadwiger's characterization theorem
Hadwiger's theorem asserts that every valuation (measure theory)Valuation (measure theory)
In measure theory or at least in the approach to it through domain theory, a valuation is a map from the class of open sets of a topological space to the set positive real numbers including infinity...
on convex bodies in Rn that is continuous and invariant under rigid motions of Rn is a linear combination of the quermassintegrals (or, equivalently, of the intrinsic volumes).