
Valuation (measure theory)
Encyclopedia
In measure theory or at least in the approach to it through domain theory
, a valuation is a map
from the class of open set
s of a topological space
to the set positive real number
s including infinity
. It is a concept closely related to that of a measure
and as such it finds applications measure theory, probability theory
and also in theoretical computer science
.
 be a topological space: a valuation is any map
be a topological space: a valuation is any map
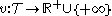
satisfying the following three properties
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
, a valuation is a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from the class of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
to the set positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s including infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. It is a concept closely related to that of a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
and as such it finds applications measure theory, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and also in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
.
Domain/Measure theory definition
Let be a topological space: a valuation is any map
be a topological space: a valuation is any map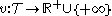
satisfying the following three properties
-
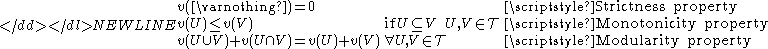
The definition immediately shows the relationship between a valuation and a measure: the properties of the two mathematical object are often very similar if not identical, the only difference being that the domain of a measure is the Borel algebraBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of the given topological space, while the domain of a valuation is the class of open sets. Further details and references can be found in and .
Continuous valuation
A valuation (as defined in domain theory/measure theory) is said to be continuous if for every directed family of open sets (i.e. an indexed familyIndexed familyIn mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of open sets (i.e. an indexed familyIndexed familyIn mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of open sets which is also directedDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
in the sense that for each pair of indexes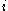 and
and 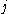 belonging to the index setIndex setIn mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
belonging to the index setIndex setIn mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
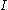 , there exists an index
, there exists an index 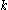 such that
such that 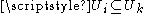 and
and  ) the following equality holds:
) the following equality holds:

Simple valuation
A valuation (as defined in domain theory/measure theory) is said to be simple if it is a finite linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
with non-negative coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of Dirac valuations, i.e.
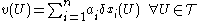
where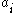 is always greather than or al least equal to zero for all index
is always greather than or al least equal to zero for all index 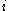 . Simple valuations are obviously continuous in the above sense. The supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
. Simple valuations are obviously continuous in the above sense. The supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of a directed family of simple valuations (i.e. an indexed family of simple valuations which is also directed in the sense that for each pair of indexes and
and 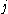 belonging to the index set
belonging to the index set 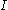 , there exists an index
, there exists an index 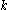 such that
such that 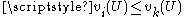 and
and 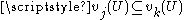 ) is called quasi-simple valuation
) is called quasi-simple valuation
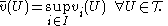
See also
- The extension problem for a given valuation (in the sense of domain theory/measure theory) consists in finding under what type of conditions it can be extended to a measure on a proper topological space, which may or may not be the same space where it is defined: the papers and in the reference section are devoted to this aim and give also several historical details.
- The concepts of valuation on convex setConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s and valuation on manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s are a generalization of valuation in the sense of domainDomain theoryDomain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
/measure theory. A valuation on convex sets is allowed to assume complex valuesComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, and the underlying topological space is the set of non-empty convex compact subsets of a finite-dimensional vector space: a valuation on manifolds is a complex valued finitely additive measure defined on a proper subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the class of all compact submanifolds of the given manifolds. Details can be found in several arxivArXivThe arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
papers of prof. Semyon Alesker.
Dirac valuation
Let be a topological space, and let
be a topological space, and let  be a point of
be a point of 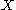 : the map
: the map
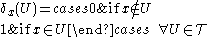
is a valuation in the domain theory/measure theory, sense called DiracPaul DiracPaul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
valuation. This concept bears its origin from distribution theoryDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
as it is an obvious transposition to valuation theory of Dirac distribution: as seen above, Dirac valuations are the "brickBrickA brick is a block of ceramic material used in masonry construction, usually laid using various kinds of mortar. It has been regarded as one of the longest lasting and strongest building materials used throughout history.-History:...
s" simple valuations are made of.
External links
- Alesker, Semyon, "various preprints on valuation s", arxivArXivThe arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
preprint server, primary site at Cornell UniversityCornell UniversityCornell University is an Ivy League university located in Ithaca, New York, United States. It is a private land-grant university, receiving annual funding from the State of New York for certain educational missions...
. Several papers dealing with valuations on convex sets, valuations on manifolds and related topics.

