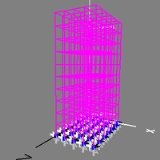
Modal analysis using FEM
Encyclopedia
The goal of modal analysis
in structural mechanics is to determine the natural mode shapes and frequencies of an object or structure during free vibration. It is common to use the finite element method
(FEM) to perform this analysis because, like other calculations using the FEM, the object being analyzed can have arbitrary shape and the results of the
calculations are acceptable. The types of equations which arise from modal analysis are those seen in eigensystems. The physical interpretation of the eigenvalues and eigenvectors which come from solving the system are that
they represent the frequencies and corresponding mode shapes. Sometimes, the only desired modes are the lowest frequencies because they can be the most prominent modes at which the object will vibrate, dominating all the higher frequency
modes.
It is also possible to test a physical object to determine its natural frequencies and mode shapes. This is called an Experimental Modal Analysis
. The results of the physical test can be used to calibrate a finite element model to determine if the underlying assumptions made were correct (for example, correct material properties and boundary conditions were used).
,
the matrix
equations take the form of a dynamic three dimensional spring mass system.
The generalized equation of motion is given as:
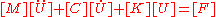
where
is the mass matrix,
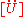is the 2nd time derivative of the displacement
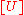(i.e., the acceleration), 
is the velocity,
is a damping matrix,
is the stiffness matrix, and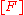 
is the force vector. The general problem, with nonzero damping, is a quadratic eigenvalue problem. However, for vibrational modal analysis, the damping is generally ignored, leaving only the 1st and 3rd terms on the left hand side:
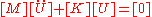
This is the general form of the eigensystem encountered in structural
engineering using the FEM
. To represent the free-vibration solutions of the structure harmonic motion is assumed , so that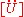
is taken to equal
,
where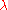
is an eigenvalue (with units of reciprocal time squared, e.g., 
),
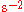and the equation reduces to:
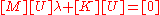
In contrast, the equation for static problems is:
which is expected when all terms having a time derivative are set to zero.
, it is more common to see the standard form of an eigensystem which is
expressed as:
Both equations can be seen as the same because if the general equation is
multiplied through by the inverse of the mass,
,
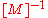it will take the form of the latter.
Because the lower modes are desired, solving the system
more likely involves the equivalent of multiplying through by the inverse of the stiffness,
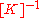, a process called inverse iteration
.
When this is done, the resulting eigenvalues,
, relate to that of the original by:
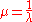
but the eigenvectors are the same.
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
in structural mechanics is to determine the natural mode shapes and frequencies of an object or structure during free vibration. It is common to use the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
(FEM) to perform this analysis because, like other calculations using the FEM, the object being analyzed can have arbitrary shape and the results of the
calculations are acceptable. The types of equations which arise from modal analysis are those seen in eigensystems. The physical interpretation of the eigenvalues and eigenvectors which come from solving the system are that
they represent the frequencies and corresponding mode shapes. Sometimes, the only desired modes are the lowest frequencies because they can be the most prominent modes at which the object will vibrate, dominating all the higher frequency
modes.
It is also possible to test a physical object to determine its natural frequencies and mode shapes. This is called an Experimental Modal Analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
. The results of the physical test can be used to calibrate a finite element model to determine if the underlying assumptions made were correct (for example, correct material properties and boundary conditions were used).
FEA eigensystems
For the most basic problem involving a linear elastic material which obeys Hooke's LawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
,
the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
equations take the form of a dynamic three dimensional spring mass system.
The generalized equation of motion is given as:
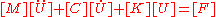
where
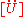is the mass matrix, is the 2nd time derivative of the displacement 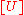(i.e., the acceleration), is the velocity,
is a damping matrix, is the stiffness matrix, and 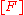is the force vector. The general problem, with nonzero damping, is a quadratic eigenvalue problem. However, for vibrational modal analysis, the damping is generally ignored, leaving only the 1st and 3rd terms on the left hand side:
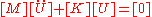
This is the general form of the eigensystem encountered in structural
engineering using the FEM
FEM
FEM refers to a number of things, either as an acronym or otherwise:*Field emission microscopy*Finite element method*FEM *[Front End Module ]*Far East Movement*fem - alternative spelling of femme...
. To represent the free-vibration solutions of the structure harmonic motion is assumed , so that
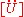
is taken to equal
,where
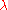is an eigenvalue (with units of reciprocal time squared, e.g., 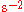),and the equation reduces to:
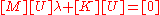
In contrast, the equation for static problems is:
which is expected when all terms having a time derivative are set to zero.
Comparison to linear algebra
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, it is more common to see the standard form of an eigensystem which is
expressed as:
Both equations can be seen as the same because if the general equation is
multiplied through by the inverse of the mass,
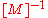,it will take the form of the latter.
Because the lower modes are desired, solving the system
more likely involves the equivalent of multiplying through by the inverse of the stiffness,
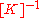, a process called inverse iterationInverse iteration
In numerical analysis, inverse iteration is an iterative eigenvalue algorithm. It allows to find an approximateeigenvector when an approximation to a corresponding eigenvalue is already known....
.
When this is done, the resulting eigenvalues,
, relate to that of the original by: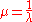but the eigenvectors are the same.
See also
- Finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
- Finite element method in structural mechanicsFinite element method in structural mechanicsThe Finite element method is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at...
- Modal analysisModal analysisModal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
- Seismic analysisSeismic analysisSeismic Analysis is a subset of structural analysis and is the calculation of the response of a building structure to earthquakes...
- Structural DynamicsStructural DynamicsStructural dynamics is a subset of structural analysis which covers the behaviour of structures subjected to dynamic loading. Dynamic loads include people, wind, waves, traffic, earthquakes, and blasts. Any structure can be subject to dynamic loading. Dynamic analysis can be used to find dynamic...
- Eigensystem
- Eigenmode
- Quadratic eigenvalue problem
- Modal Analysis for deformation simulation