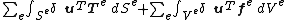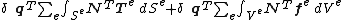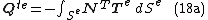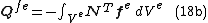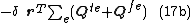
Finite element method in structural mechanics
Encyclopedia
The Finite element method
(FEM) is a powerful technique originally developed for numerical solution of complex problems in structural mechanics
, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion, density
, Young's modulus
, shear modulus and Poisson's ratio
.
and Clough
became foundation for today’s finite element structural analysis methods. Earlier books such as by Zienkiewicz
and more recent books such as by Yang give comprehensive summary of developments in finite-element structural analysis.
or degrees of freedom
which may include translations, rotations, and for special applications, higher order derivative
s of displacements. When the nodes displace, they will drag the elements along in a certain manner dictated by the element formulation. In other words, displacements of any points in the element will be interpolated
from the nodal displacements, and this is the main reason for the approximate nature of the solution.
Large scale commercial software packages often provide facilities for generating the mesh, graphical display of input and output, which greatly facilitate the verification of both input data and interpretation of the results.
follows the more traditional approach via the virtual work
principle or the minimum total potential energy principle
. The virtual work
principle approach is more general as it is applicable to both linear and non-linear material behaviours.
The principle of virtual displacements
for the structural system expresses the mathematical identity of external and internal virtual work: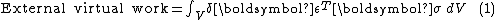
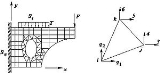
The virtual internal work in the right-hand-side of the above equation may be found by summing the virtual work in the individual elements—This is the crucial step where we will need displacement functions written only for the small domain rather than over the entire system. As shown in the subsequent sections, Eq.(1) leads to the following governing equilibrium equation for the system:
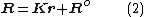
where = vector of nodal forces, representing external forces applied to the system's nodes.
= vector of nodal forces, representing external forces applied to the system's nodes. = vector of system's nodal displacements, which will, by interpolation, yield displacements at any point of the finite element mesh.
= vector of system's nodal displacements, which will, by interpolation, yield displacements at any point of the finite element mesh.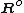 = vector of equivalent nodal forces, representing all external effects other than the nodal forces which are already included in the preceding nodal force vector R. These external effects may include distributed or concentrated surface forces, body forces, thermal effects, initial stresses and strains.
= vector of equivalent nodal forces, representing all external effects other than the nodal forces which are already included in the preceding nodal force vector R. These external effects may include distributed or concentrated surface forces, body forces, thermal effects, initial stresses and strains.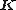 = system stiffness matrix, which will be established by assembling the elements' stiffness matrices :
= system stiffness matrix, which will be established by assembling the elements' stiffness matrices :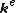 .
.
Once the supports' constraints are accounted for, the nodal displacements are found by solving the system of linear equations (2), symbolically: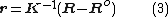
Subsequently, the strains and stresses in individual elements may be found as follows:
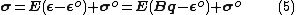
where = vector of element's nodal displacements--a subset of the system displacement vector r that pertains to the element under consideration.
= vector of element's nodal displacements--a subset of the system displacement vector r that pertains to the element under consideration.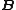 = strain-displacement matrix that transforms nodal displacements q to strains at any point in the element.
= strain-displacement matrix that transforms nodal displacements q to strains at any point in the element.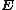 = elasticity matrix that transforms effective strains to stresses at any point in the element.
= elasticity matrix that transforms effective strains to stresses at any point in the element.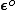 = vector of initial strains in the element.
= vector of initial strains in the element.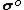 = vector of initial stresses in the element.
= vector of initial stresses in the element.
By applying the virtual work
equation (1) to the system, we can establish the element matrices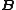 ,
, 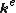 as well as the technique of assembling the system matrices
as well as the technique of assembling the system matrices 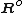 and
and 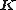 . Other matrices such as
. Other matrices such as 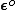 ,
, 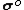 ,
, 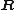 and
and 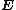 can be directly set up from data input.
can be directly set up from data input.
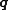 be the vector of nodal displacements of a typical element. The displacements at any point of the element may be found by interpolation
be the vector of nodal displacements of a typical element. The displacements at any point of the element may be found by interpolation
functions as, symbolically: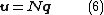
where = vector of displacements at any point {x,y,z} of the element.
= vector of displacements at any point {x,y,z} of the element.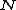 = matrix of shape functions serving as interpolation
= matrix of shape functions serving as interpolation
functions.
Equation (6) gives rise to other quantities of great interest:
 , the internal virtual work due to virtual displacements is obtained by substitution of (5) and (9) into (1):
, the internal virtual work due to virtual displacements is obtained by substitution of (5) and (9) into (1):
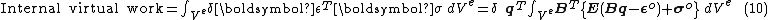
These matrices are usually evaluated numerically using Gaussian quadrature
for numerical integration
.
Their use simplifies (10) to the following: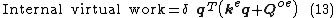
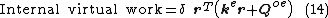
where, for simplicity, we use the same symbols for the element matrices, which now have expanded size as well as suitably rearranged rows and columns.
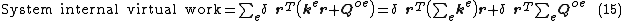
Considering now the left-hand-side of (1), the system external virtual work consists of:
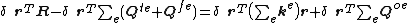
Since the virtual displacements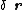 are arbitrary, the preceding equality reduces to:
are arbitrary, the preceding equality reduces to:
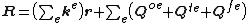
Comparison with (2) shows that:
In practice, the element matrices are neither expanded nor rearranged. Instead, the system stiffness matrix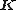 is assembled by adding individual coefficients
is assembled by adding individual coefficients 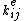 to
to 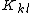 where the subscripts ij, kl mean that the element's nodal displacements
where the subscripts ij, kl mean that the element's nodal displacements 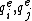 match respectively with the system's nodal displacements
match respectively with the system's nodal displacements 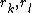 . Similarly,
. Similarly, 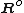 is assembled by adding individual coefficients
is assembled by adding individual coefficients 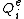 to
to 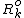 where
where 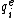 matches
matches 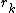 . This direct addition of
. This direct addition of 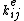 into
into 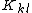 gives the procedure the name Direct Stiffness Method
gives the procedure the name Direct Stiffness Method
.
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
(FEM) is a powerful technique originally developed for numerical solution of complex problems in structural mechanics
Structural mechanics
Structural mechanics or Mechanics of structures is the computation of deformations, deflections, and internal forces or stresses within structures, either for design or for performance evaluation of existing structures. It is one subset of structural analysis...
, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion, density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
, shear modulus and Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
.
History
The origin of finite method can be traced to the matrix analysis of structures where the concept of displacement or stiffness matrix approach was introduced. Finite element concepts were developed based on engineering methods in 50s. The original works such as those by ArgyrisJohn Argyris
John Hadji Argyris was among the creators of the Finite Element Method and lately Professor at the University of Stuttgart and Director of the Institute for Statics and Dynamics of Aerospace Structures. His uncle, Constantin Carathéodory, was a Greek mathematician of the Modern Era...
and Clough
Ray W. Clough
Ray William Clough, , was Byron L. and Elvira E. Nishkian Professor of Structural Engineering in the department of Civil Engineering at the University of California, Berkeley and one the founders of the Finite Element Method . His article in 1956 was one of the first applications of this...
became foundation for today’s finite element structural analysis methods. Earlier books such as by Zienkiewicz
Olgierd Zienkiewicz
Olgierd Cecil Zienkiewicz, CBE, FREng, FRS was a British academic, mathematician, and civil engineer. He was born in Caterham, England. He was one of the early pioneers of the finite element method...
and more recent books such as by Yang give comprehensive summary of developments in finite-element structural analysis.
Element properties
- Straight or curved one-dimensional elements with physical properties such as axial, bending, and torsional stiffnesses. This type of elements is suitable for modeling cables, braces, trusses, beams, stiffeners, grids and frames. Straight elements usually have two nodes, one at each end, while curved elements will need at least three nodes including the end-nodes. The elements are positioned at the centroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
al axis of the actual members. - Two-dimensional elements for membrane action (plane stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
, plane strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
) and/or bending action (plates and shellsThin-shell structureThin-shell structures are light weight constructions using shell elements. These elements are typically curved and are assembled to large structures...
). They may have a variety of shapes such as flat or curved triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
s. Nodes are usually placed at the element corners and, if needed for higher accuracy, additional nodes can be placed along the element edges or even inside the element. The elements are positioned at the mid-surface of the actual layer thickness. - TorusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
-shaped elements for axisymmetric problems such as thin, thick plates, shells, and solids. The cross-section of the elements are similar to the previously described types: one-dimensional for thin plates and shells, and two-dimensional for solids, and thick plates and shells. - Three-dimensional elements for modeling 3-D solids such as machineMachineA machine manages power to accomplish a task, examples include, a mechanical system, a computing system, an electronic system, and a molecular machine. In common usage, the meaning is that of a device having parts that perform or assist in performing any type of work...
components, damDamA dam is a barrier that impounds water or underground streams. Dams generally serve the primary purpose of retaining water, while other structures such as floodgates or levees are used to manage or prevent water flow into specific land regions. Hydropower and pumped-storage hydroelectricity are...
s, embankmentEmbankment (transportation)To keep a road or railway line straight or flat, and where the comparative cost or practicality of alternate solutions is prohibitive, the land over which the road or rail line will travel is built up to form an embankment. An embankment is therefore in some sense the opposite of a cutting, and...
s or soil masses. Common element shapes include tetrahedrals and hexahedrals. Nodes are placed at the vertexes and possibly in the element faces or within the element.
Element interconnection and displacement
The elements are interconnected only at the exterior nodes, and altogether they should cover the entire domain as accurately as possible. Nodes will have nodal (vector) displacementsDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
or degrees of freedom
Degrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
which may include translations, rotations, and for special applications, higher order derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of displacements. When the nodes displace, they will drag the elements along in a certain manner dictated by the element formulation. In other words, displacements of any points in the element will be interpolated
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
from the nodal displacements, and this is the main reason for the approximate nature of the solution.
Practical considerations
From the application point of view, it is important to model the system such that:- Symmetry or anti-symmetry conditions are exploited in order to reduce the size of the domain.
- Displacement compatibility, including any required discontinuity, is ensured at the nodes, and preferably, along the element edges as well, particularly when adjacent elements are of different types, material or thickness. Compatibility of displacements of many nodes can usually be imposed via constraint relations—When such a feature is not available in the software package, a physical model that imposes the constraints may be used instead.
- Elements' behaviours capture the dominant actions of the actual system, both locally and globally.
- The element mesh is sufficiently fine in order to have acceptable accuracy. To assess accuracy, the mesh is refined until the important results shows little change. For higher accuracy, the aspect ratioAspect ratio (image)The aspect ratio of an image is the ratio of the width of the image to its height, expressed as two numbers separated by a colon. That is, for an x:y aspect ratio, no matter how big or small the image is, if the width is divided into x units of equal length and the height is measured using this...
of the elements should be as close to unity as possible, and smaller elements are used over the parts of higher stress gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
. - Proper support constraints are imposed with special attention paid to nodes on symmetry axes.
Large scale commercial software packages often provide facilities for generating the mesh, graphical display of input and output, which greatly facilitate the verification of both input data and interpretation of the results.
Theoretical overview of FEM-Displacement Formulation: From elements to system to solution
While the theory of FEM can be presented in different perspectives or emphases, its development for structural analysisStructural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
follows the more traditional approach via the virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
principle or the minimum total potential energy principle
Minimum total potential energy principle
The principle of minimum total potential energy is a fundamental concept used in physics, chemistry, biology, and engineering. It asserts that a structure or body shall deform or displace to a position that minimizes the total potential energy, with the lost potential energy being dissipated as heat...
. The virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
principle approach is more general as it is applicable to both linear and non-linear material behaviours.
The principle of virtual displacements
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
for the structural system expresses the mathematical identity of external and internal virtual work:
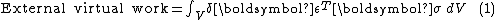
The virtual internal work in the right-hand-side of the above equation may be found by summing the virtual work in the individual elements—This is the crucial step where we will need displacement functions written only for the small domain rather than over the entire system. As shown in the subsequent sections, Eq.(1) leads to the following governing equilibrium equation for the system:
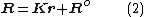
where
 = vector of nodal forces, representing external forces applied to the system's nodes.
= vector of nodal forces, representing external forces applied to the system's nodes. = vector of system's nodal displacements, which will, by interpolation, yield displacements at any point of the finite element mesh.
= vector of system's nodal displacements, which will, by interpolation, yield displacements at any point of the finite element mesh.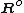 = vector of equivalent nodal forces, representing all external effects other than the nodal forces which are already included in the preceding nodal force vector R. These external effects may include distributed or concentrated surface forces, body forces, thermal effects, initial stresses and strains.
= vector of equivalent nodal forces, representing all external effects other than the nodal forces which are already included in the preceding nodal force vector R. These external effects may include distributed or concentrated surface forces, body forces, thermal effects, initial stresses and strains.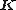 = system stiffness matrix, which will be established by assembling the elements' stiffness matrices :
= system stiffness matrix, which will be established by assembling the elements' stiffness matrices :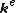 .
.Once the supports' constraints are accounted for, the nodal displacements are found by solving the system of linear equations (2), symbolically:
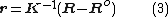
Subsequently, the strains and stresses in individual elements may be found as follows:

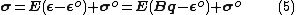
where
 = vector of element's nodal displacements--a subset of the system displacement vector r that pertains to the element under consideration.
= vector of element's nodal displacements--a subset of the system displacement vector r that pertains to the element under consideration.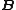 = strain-displacement matrix that transforms nodal displacements q to strains at any point in the element.
= strain-displacement matrix that transforms nodal displacements q to strains at any point in the element.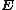 = elasticity matrix that transforms effective strains to stresses at any point in the element.
= elasticity matrix that transforms effective strains to stresses at any point in the element.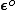 = vector of initial strains in the element.
= vector of initial strains in the element.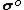 = vector of initial stresses in the element.
= vector of initial stresses in the element.By applying the virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
equation (1) to the system, we can establish the element matrices
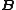 ,
, 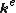 as well as the technique of assembling the system matrices
as well as the technique of assembling the system matrices 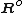 and
and 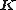 . Other matrices such as
. Other matrices such as 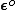 ,
, 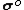 ,
, 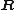 and
and 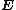 can be directly set up from data input.
can be directly set up from data input.Interpolation or shape functions
Let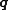 be the vector of nodal displacements of a typical element. The displacements at any point of the element may be found by interpolation
be the vector of nodal displacements of a typical element. The displacements at any point of the element may be found by interpolationInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
functions as, symbolically:
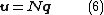
where
 = vector of displacements at any point {x,y,z} of the element.
= vector of displacements at any point {x,y,z} of the element.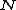 = matrix of shape functions serving as interpolation
= matrix of shape functions serving as interpolationInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
functions.
Equation (6) gives rise to other quantities of great interest:
- Virtual displacements consistent with virtual nodal displacements:
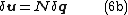
- Strains in the elements:
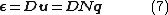
- where
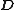 = matrix of differential operators that convert displacements to strains using linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
= matrix of differential operators that convert displacements to strains using linear elasticityLinear elasticityLinear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
theory. Eq.(7) shows that matrix B in (4) is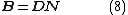
- Virtual strains consistent with element's virtual nodal displacements:

- Virtual strains consistent with element's virtual nodal displacements:
Internal virtual work in a typical element
For a typical element of volume , the internal virtual work due to virtual displacements is obtained by substitution of (5) and (9) into (1):
, the internal virtual work due to virtual displacements is obtained by substitution of (5) and (9) into (1):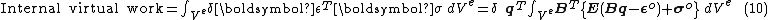
Element matrices
Primarily for the convenience of reference, the following matrices pertaining to a typical elements may now be defined:- Element stiffness matrix
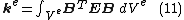
- Equivalent element load vector
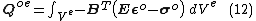
These matrices are usually evaluated numerically using Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
for numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
.
Their use simplifies (10) to the following:
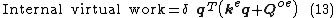
Element virtual work in terms of system nodal displacements
Since the nodal displacement vector q is a subset of the system nodal displacements r (for compatibility with adjacent elements), we can replace q with r by expanding the size of the element matrices with new columns and rows of zeros: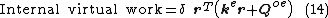
where, for simplicity, we use the same symbols for the element matrices, which now have expanded size as well as suitably rearranged rows and columns.
System virtual work
Summing the internal virtual work (14) for all elements gives the right-hand-side of (1):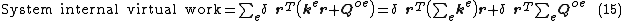
Considering now the left-hand-side of (1), the system external virtual work consists of:
- The work done by the nodal forces R:
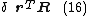
- The work done by external forces
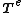 on the part
on the part 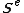 of the elements' edges or surfaces, and by the body forces
of the elements' edges or surfaces, and by the body forces 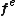
-
- Substitution of (6b) gives:
-
- or
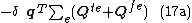
- where we have introduced additional element's matrices defined below:
-
- Again, numerical integrationNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
is convenient for their evaluation. A similar replacement of q in (17a) with r gives, after rearranging and expanding the vectors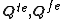 :
:
Assembly of system matrices
Adding (16), (17b) and equating the sum to (15) gives: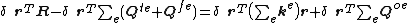
Since the virtual displacements
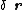 are arbitrary, the preceding equality reduces to:
are arbitrary, the preceding equality reduces to: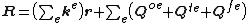
Comparison with (2) shows that:
- The system stiffness matrix is obtained by summing the elements' stiffness matrices:
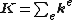
- The vector of equivalent nodal forces is obtained by summing the elements' load vectors:

In practice, the element matrices are neither expanded nor rearranged. Instead, the system stiffness matrix
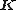 is assembled by adding individual coefficients
is assembled by adding individual coefficients 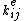 to
to 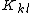 where the subscripts ij, kl mean that the element's nodal displacements
where the subscripts ij, kl mean that the element's nodal displacements 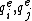 match respectively with the system's nodal displacements
match respectively with the system's nodal displacements 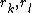 . Similarly,
. Similarly, 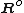 is assembled by adding individual coefficients
is assembled by adding individual coefficients 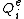 to
to 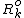 where
where 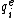 matches
matches 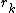 . This direct addition of
. This direct addition of 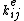 into
into 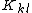 gives the procedure the name Direct Stiffness Method
gives the procedure the name Direct Stiffness MethodDirect stiffness method
As one of the methods of structural analysis, the direct stiffness method , also known as the displacement method or matrix stiffness method, is particularly suited for computer-automated analysis of complex structures including the statically indeterminate type...
.
See also
- Finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
- Flexibility methodFlexibility methodIn structural engineering, the flexibility method is the classical consistent deformation method for computing member forces and displacements in structural systems...
- Matrix stiffness method
- Modal analysis using FEMModal analysis using FEMThe goal of modal analysis in structural mechanics is to determine the natural mode shapes and frequencies of an object or structure during free vibration. It is common to use the finite element method to perform this analysis because, like other calculations using the FEM, the object being...
- List of finite element software packages
- Structural analysisStructural analysisStructural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
- Virtual workVirtual workVirtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
- Interval finite elementInterval finite elementThe interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics,...