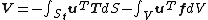Minimum total potential energy principle
Encyclopedia
The principle of minimum total potential energy is a fundamental concept used in physics
, chemistry
, biology
, and engineering
. It asserts that a structure or body shall deform or displace to a position that minimizes the total potential energy, with the lost potential energy being dissipated as heat. For example, a marble placed in a bowl will move to the bottom and rest there, and similarly, a tree branch laden with snow will bend to a lower position. The lower position is the position for minimum potential energy: it is the stable configuration for equilibrium. The principle has many applications in structural analysis
and solid mechanics
.
The tendency to minimum total potential energy is due to the second law of thermodynamics
, which states that the entropy
of a system will maximize at equilibrium. Given two possibilities - a low heat content and a high potential energy, or a high heat content and low potential energy, the latter will be the state with the highest entropy, and will therefore be the state towards which the system moves.
The principle of minimum total potential energy should not be confused with the related principle of minimum energy
which states that for a system that changes
without heat transfer, the total energy will be minimized.
Note that in most complex systems there is one global minimum and many local minima (smaller dips) in the potential energy. These are called metastable
states. A system may reside in a local minimum for a long time — even an effectively infinite period of time.
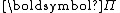, is the sum of the elastic strain energy, U, stored in the deformed body and the potential energy, V, of the applied forces: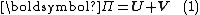
This energy is at a stationary position
when an infinitesimal
variation from such position involves no change in energy:
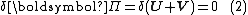
The principle of minimum total potential energy may be derived as a special case of the virtual work
principle for elastic systems subject to conservative force
s.
The equality between external and internal virtual work (due to virtual displacements) is:
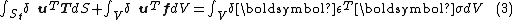
where
In the special case of elastic bodies, the right-hand-side of (3) can be taken to be the change,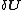
, of elastic strain energy U due to infinitesimal variations of real displacements.
In addition, when the external forces are conservative force
s, the left-hand-side of (3) can be seen as the change in the potential energy
function V of the forces. The function V is defined as:
where the minus sign implies a loss of potential energy as the force is displaced in its direction. With these two subsidiary conditions, (3) becomes:
This leads to (2) as desired. The variational form of (2) is often used as the basis for developing the finite element method in structural mechanics
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
. It asserts that a structure or body shall deform or displace to a position that minimizes the total potential energy, with the lost potential energy being dissipated as heat. For example, a marble placed in a bowl will move to the bottom and rest there, and similarly, a tree branch laden with snow will bend to a lower position. The lower position is the position for minimum potential energy: it is the stable configuration for equilibrium. The principle has many applications in structural analysis
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
and solid mechanics
Solid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
.
The tendency to minimum total potential energy is due to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, which states that the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a system will maximize at equilibrium. Given two possibilities - a low heat content and a high potential energy, or a high heat content and low potential energy, the latter will be the state with the highest entropy, and will therefore be the state towards which the system moves.
The principle of minimum total potential energy should not be confused with the related principle of minimum energy
Principle of minimum energy
The principle of minimum energy is essentially a restatement of the second law of thermodynamics. It states that for a closed system, with constant external parameters and entropy, the internal energy will decrease and approach a minimum value at equilibrium...
which states that for a system that changes
without heat transfer, the total energy will be minimized.
Note that in most complex systems there is one global minimum and many local minima (smaller dips) in the potential energy. These are called metastable
Metastability
Metastability describes the extended duration of certain equilibria acquired by complex systems when leaving their most stable state after an external action....
states. A system may reside in a local minimum for a long time — even an effectively infinite period of time.
Some examples
- A free protonProtonThe proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
and free electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
will tend to combine to form the lowest energy state (the ground stateGround stateThe ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
) of a hydrogen atomHydrogen atomA hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, the most stable configurationElectron configurationIn atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
. This is because that state's energy is 13.6 electron volts (eV)ElectronvoltIn physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
lower than when the two particlesElementary particleIn particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
separated by an infiniteInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
distanceDistanceDistance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
. The dissipation in this system takes the form of spontaneous emissionSpontaneous emissionSpontaneous emission is the process by which a light source such as an atom, molecule, nanocrystal or nucleus in an excited state undergoes a transition to a state with a lower energy, e.g., the ground state and emits a photon...
of electromagnetic radiationElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
, which increases the entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the surroundings.
- A rolling ball will end up stationary at the bottom of a hill, the point of minimum potential energy. The reason is that as it rolls downward under the influence of gravity, frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
produced by its motion adds to the heat of the surroundings with an attendant increase in entropy.
- A proteinProteinProteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
folds into the state of lowest potential energyPotential energy of proteinPotential Energy of Protein =A protein folds into the state of lowest potential energy. Potential energy of a protein can be evaluated with quantum chemistry. However required computation is too much...
. In this case, the dissipation takes the form of vibration of atoms within or adjacent to the protein.
Structural Mechanics
The total potential energy,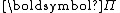, is the sum of the elastic strain energy, U, stored in the deformed body and the potential energy, V, of the applied forces: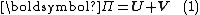This energy is at a stationary position
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
when an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
variation from such position involves no change in energy:
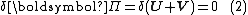
The principle of minimum total potential energy may be derived as a special case of the virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
principle for elastic systems subject to conservative force
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
s.
The equality between external and internal virtual work (due to virtual displacements) is:
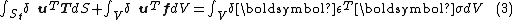
where
-
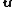= vector of displacements -
= vector of distributed forces acting on the part 
of the surface -
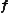= vector of body forces
In the special case of elastic bodies, the right-hand-side of (3) can be taken to be the change,
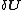, of elastic strain energy U due to infinitesimal variations of real displacements.In addition, when the external forces are conservative force
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
s, the left-hand-side of (3) can be seen as the change in the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
function V of the forces. The function V is defined as:
where the minus sign implies a loss of potential energy as the force is displaced in its direction. With these two subsidiary conditions, (3) becomes:
This leads to (2) as desired. The variational form of (2) is often used as the basis for developing the finite element method in structural mechanics
Finite element method in structural mechanics
The Finite element method is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at...
.