Modern Arabic mathematical notation
Encyclopedia
The designation modern Arabic mathematical notation is used for a mathematical notation
based on the Arabic script that is widely used in the Arab world
, especially at pre-university levels of education. Its form is mostly derived from Western notation, but has some notable features that set it apart from its Western counterpart. The most remarkable of those features is the fact that it is written from right to left following the normal direction of the Arabic script. Other differences include the replacement of the Latin alphabet
letters for symbols with Arabic letters and the use of Arabic names for functions and relations.
The notation mainly differs in numeral system used, and in mathematical symbol used
e.g.
e.g.
Mathematical constants and units
Arithmetic
 is added to the end of trigonometric functions to express hyperbolic functions (the same way h is used in Latin notation).
is added to the end of trigonometric functions to express hyperbolic functions (the same way h is used in Latin notation).

 is the one used in Arabic notation for the inverse functions like:
is the one used in Arabic notation for the inverse functions like:


Calculus
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
based on the Arabic script that is widely used in the Arab world
Arab world
The Arab world refers to Arabic-speaking states, territories and populations in North Africa, Western Asia and elsewhere.The standard definition of the Arab world comprises the 22 states and territories of the Arab League stretching from the Atlantic Ocean in the west to the Arabian Sea in the...
, especially at pre-university levels of education. Its form is mostly derived from Western notation, but has some notable features that set it apart from its Western counterpart. The most remarkable of those features is the fact that it is written from right to left following the normal direction of the Arabic script. Other differences include the replacement of the Latin alphabet
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
letters for symbols with Arabic letters and the use of Arabic names for functions and relations.
Some features of Arabic mathematical notation
- The most remarkable of those features is the fact that it is written from right to left following the normal direction of the Arabic script. Other differences include the replacement of the Latin alphabetLatin alphabetThe Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
letters for symbols with Arabic letters and the use of Arabic names for functions and relations.
- The notation exhibits one of the very few remaining vestiges of non-dotted Arabic scripts, as dots over and under letters (I'jam) are usually omitted.
- Letter cursivity (connectedness) of Arabic is also taken advantage of, in a few cases, to define variables using more than one letter. The most widespread example of this kind of usage is the canonical symbol for the radius of a circle نق (nɑq), which is written using the two letters nūnNun (letter)Nun is the fourteenth letter of many Semitic abjads, including Phoenician, Aramaic, Hebrew and Arabic alphabet . It is the third letter in Thaana , pronounced as "noonu"...
and qāfQafQaf may mean:* Qāf , a letter in the Arabic alphabet.** the Surat Qaf of the Qur'an* Ka with descender , a letter in the Kazakh, Uzbek, and Abkhaz alphabets* Jabal Qaf or Mount Qaf, a mythical mountain according to Muslim tradition....
. When variable names are juxtaposed (as when expressing multiplication) they are written non-cursively.
Arabic mathematical notation in different regions
The notation differs slightly from region to another. In university-level education most regions use the Western notation.The notation mainly differs in numeral system used, and in mathematical symbol used
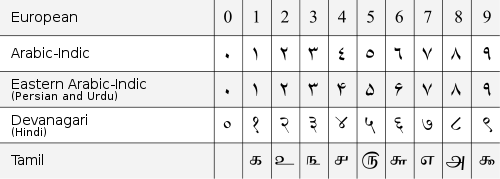
Numeral systems used in Arabic mathematical notation
There are three numeral systems used in right to left mathematical notation.- "Western Arabic numerals" (sometimes called European) are used in western Arabic regions (e.g. MoroccoMoroccoMorocco , officially the Kingdom of Morocco , is a country located in North Africa. It has a population of more than 32 million and an area of 710,850 km², and also primarily administers the disputed region of the Western Sahara...
) - "Eastern Arabic numeralsEastern Arabic numeralsThe Eastern Arabic numerals are the symbols used to represent the Hindu-Arabic numeral system in conjunction with the Arabic alphabet in the countries of the Arab world....
" are used in middle and eastern Arabic regions (e.g. EgyptEgyptEgypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
and SyriaSyriaSyria , officially the Syrian Arab Republic , is a country in Western Asia, bordering Lebanon and the Mediterranean Sea to the West, Turkey to the north, Iraq to the east, Jordan to the south, and Israel to the southwest....
) - "Eastern Arabic-Indic numerals" are used in PersianPersian languagePersian is an Iranian language within the Indo-Iranian branch of the Indo-European languages. It is primarily spoken in Iran, Afghanistan, Tajikistan and countries which historically came under Persian influence...
and UrduUrduUrdu is a register of the Hindustani language that is identified with Muslims in South Asia. It belongs to the Indo-European family. Urdu is the national language and lingua franca of Pakistan. It is also widely spoken in some regions of India, where it is one of the 22 scheduled languages and an...
speaking regions (e.g. IranIranIran , officially the Islamic Republic of Iran , is a country in Southern and Western Asia. The name "Iran" has been in use natively since the Sassanian era and came into use internationally in 1935, before which the country was known to the Western world as Persia...
, PakistanPakistanPakistan , officially the Islamic Republic of Pakistan is a sovereign state in South Asia. It has a coastline along the Arabian Sea and the Gulf of Oman in the south and is bordered by Afghanistan and Iran in the west, India in the east and China in the far northeast. In the north, Tajikistan...
, IndiaIndiaIndia , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
)

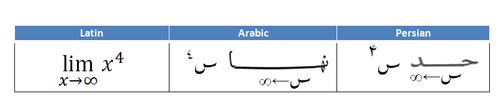
Arabic symbols and mirrored Latin symbols
- Sometimes, The symbols used in Arabic mathematical notation differs according to the region
e.g.

- Sometimes, mirrored Latin symbols are used in Arabic mathematical notation (especially in western Arabic regions)
e.g.

Mathematical letters
| Latin | Arabic |
|---|---|
 |
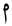 |
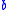 |
 |
 |
 |
 |
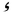 |
 |
 |
 |
 |
 |
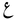 |
- Usage of Latin x in maths is derived from the first letter of the Arabic word شيء [ʃajʔ(un)] meaning thing. (X was used in old SpanishSpanish languageSpanish , also known as Castilian , is a Romance language in the Ibero-Romance group that evolved from several languages and dialects in central-northern Iberia around the 9th century and gradually spread with the expansion of the Kingdom of Castile into central and southern Iberia during the...
for the sound /ʃ/).
Mathematical constants and unitsUnits of measurementA unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
| Description | Latin | Arabic | Notes |
|---|---|---|---|
| Euler's number |  |
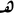 |
|
| imaginary unit Imaginary unit In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek... |
 |
 |
|
| pi Pi ' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants... |
 |
 |
also  in some regions in some regions |
| radius Radius In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its... |
 |
 |
|
| kilogram Kilogram The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water... |
kg |  |
In some regions alternative symbols like 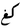 or or  are used are used |
| gram Gram The gram is a metric system unit of mass.... |
g | 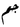 |
|
| meter | m |  |
|
| centimeter | cm |  |
|
| millimeter | mm | 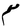 |
|
| kilometer | km |  |
also 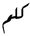 in some regions in some regions |
| second | s | 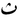 |
|
| minute | min | 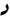 |
also  in some regions in some regions |
| hour | h |  |
|
| kilometer per hour | km/h |  |
|
| degree Celsius | °C |  |
also 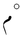 |
| degree Fahrenheit | °F | 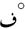 |
|
| millimeters of mercury Torr The torr is a non-SI unit of pressure with the ratio of 760 to 1 standard atmosphere, chosen to be roughly equal to the fluid pressure exerted by a millimetre of mercury, i.e., a pressure of 1 torr is approximately equal to 1 mmHg... |
mmHg | 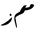 |
|
| Ångström Ångström The angstrom or ångström, is a unit of length equal to 1/10,000,000,000 of a meter . Its symbol is the Swedish letter Å.... |
Å | 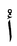 |
|
Sets and number systems
| Description | Latin | Arabic |
|---|---|---|
| Natural numbers |  |
 |
| Integers |  |
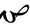 |
| Rational numbers |  |
 |
| Real numbers |  |
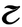 |
| Imaginary numbers | 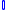 |
 |
| Complex numbers |  |
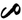 |
| Empty set Empty set In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced... |
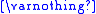 |
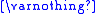 |
| Is an element of |  |
 |
| Subset Subset In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment... |
 |
 |
| Superset SuperSet SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst... |
 |
 |
| Universal set Universal set In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox... |
 |
 |
ArithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
| Description | Latin | Arabic | Notes |
|---|---|---|---|
| Decimal Point |  |
 |
a Decimal comma is used |
| Comma Comma A comma is a type of punctuation mark . The word comes from the Greek komma , which means something cut off or a short clause.Comma may also refer to:* Comma , a type of interval in music theory... |
 |
، | ، is used instead of , in Latin notation |
| Percent | % |  |
|
| Permille Permille A per mil or per mille is a tenth of a percent or one part per thousand. It is written with the sign ‰ , which looks like a percent sign with an extra zero at the end... |
‰ |  |
|
| Is proportional to Proportionality (mathematics) In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one... |
 |
 |
|
| n th root Nth root In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root... |
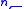 |
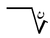 |
|
| Logarithm Logarithm The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written... |
 |
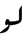 |
|
| Logarithm to base b Logarithm The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written... |
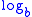 |
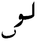 |
|
| Natural logarithm Natural logarithm The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828... |
 |
 |
|
| Summation Summation Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,... |
 |
 |
also  in some regions in some regions |
| Product Product (mathematics) In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication... |
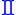 |
 |
also 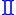 in some regions in some regions |
| factorial Factorial In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n... |
 |
 |
also  in some regions in some regions |
| permutations | 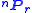 |
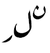 |
also .png) is used in some regions as is used in some regions as  |
| Combinations |  |
 |
also .png) is used in some regions as is used in some regions as  and .png) as the binomial coefficient as the binomial coefficientBinomial coefficient In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...  |
Trigonometric functions
| Latin | Arabic | Notes |
|---|---|---|
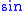 |
 |
also 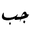 is used in some regions (e.g. : Syria) is used in some regions (e.g. : Syria) |
 |
 |
also  is used in some regions (e.g. : Syria) is used in some regions (e.g. : Syria) |
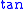 |
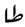 |
also  is used in some regions (e.g. : Syria) is used in some regions (e.g. : Syria) |
 |
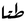 |
also  is used in some regions (e.g. : Syria) is used in some regions (e.g. : Syria) |
 |
 |
|
 |
 |
|
Hyperbolic functions
The letter is added to the end of trigonometric functions to express hyperbolic functions (the same way h is used in Latin notation).
is added to the end of trigonometric functions to express hyperbolic functions (the same way h is used in Latin notation).
Inverse trigonometric functions
The notation is the one used in Arabic notation for the inverse functions like:
is the one used in Arabic notation for the inverse functions like:
Inverse hyperbolic functions

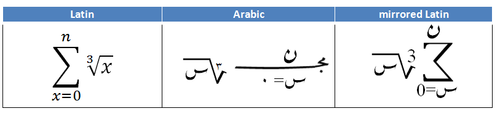
CalculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
| Description | Latin | Arabic | Notes |
|---|---|---|---|
| Limit Limit (mathematics) In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric... |
 |
 |
also  is used in some regions (e.g. Iran) is used in some regions (e.g. Iran) |
| function Function (mathematics) In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can... |
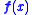 |
.png) |
|
| derivatives |  |
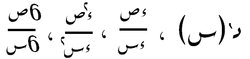 |
|
| Integrals |  |
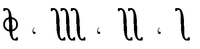 |
|
Complex analysis
| Latin | Arabic |
|---|---|
 |
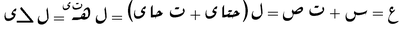 |
External links
- Multilingual mathematical e-document processing
- Arabic mathematical notation - W3C Interest Group Note.

