
Modified Richardson iteration
Encyclopedia
Modified Richardson iteration is an iterative method
for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobi
and Gauss–Seidel method.
We seek the solution to a set of linear equations, expressed in matrix terms as
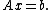
The Richardson iteration is
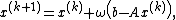
where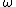 is a scalar parameter that has to be chosen such that the sequence
is a scalar parameter that has to be chosen such that the sequence 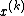 converges.
converges.
It is easy to see that the method is correct, because if it converges, then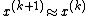 and
and 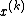 has to approximate a solution of
has to approximate a solution of 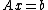 .
.
 , and introducing the notation for the error
, and introducing the notation for the error 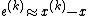 , we get the equality for the errors
, we get the equality for the errors
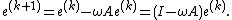
Thus,
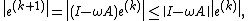
for any vector norm and the corresponding induced matrix norm. Thus, if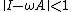 the method convergences.
the method convergences.
Suppose that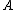 is diagonalizable and that
is diagonalizable and that 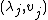 are the eigenvalues and eigenvectors of
are the eigenvalues and eigenvectors of 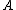 . The error converges to
. The error converges to 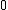 if
if 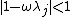 for all eigenvalues
for all eigenvalues 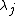 . If, e.g., all eigenvalues are positive, this can be guaranteed if
. If, e.g., all eigenvalues are positive, this can be guaranteed if 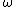 is chosen such that
is chosen such that 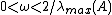 . The optimal choice, minimizing all
. The optimal choice, minimizing all 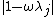 , is
, is 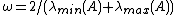 , which gives the simplest Chebyshev iteration
, which gives the simplest Chebyshev iteration
.
If there are both positive and negative eigenvalues, the method will diverge for any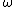 if the initial error
if the initial error 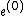 has nonzero components in the corresponding eigenvectors.
has nonzero components in the corresponding eigenvectors.
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobi
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
and Gauss–Seidel method.
We seek the solution to a set of linear equations, expressed in matrix terms as
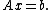
The Richardson iteration is
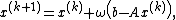
where
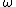 is a scalar parameter that has to be chosen such that the sequence
is a scalar parameter that has to be chosen such that the sequence 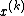 converges.
converges.It is easy to see that the method is correct, because if it converges, then
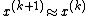 and
and 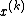 has to approximate a solution of
has to approximate a solution of 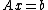 .
.Convergence
Subtracting the exact solution , and introducing the notation for the error
, and introducing the notation for the error 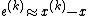 , we get the equality for the errors
, we get the equality for the errors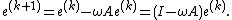
Thus,
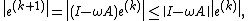
for any vector norm and the corresponding induced matrix norm. Thus, if
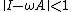 the method convergences.
the method convergences.Suppose that
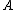 is diagonalizable and that
is diagonalizable and that 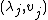 are the eigenvalues and eigenvectors of
are the eigenvalues and eigenvectors of 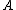 . The error converges to
. The error converges to 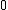 if
if 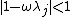 for all eigenvalues
for all eigenvalues 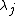 . If, e.g., all eigenvalues are positive, this can be guaranteed if
. If, e.g., all eigenvalues are positive, this can be guaranteed if 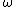 is chosen such that
is chosen such that 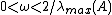 . The optimal choice, minimizing all
. The optimal choice, minimizing all 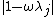 , is
, is 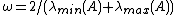 , which gives the simplest Chebyshev iteration
, which gives the simplest Chebyshev iterationChebyshev iteration
In numerical linear algebra, the Chebyshev iteration is aniterative method for determining the solutions of a system of linear equations. The method is named after Russian mathematician Pafnuty Chebyshev....
.
If there are both positive and negative eigenvalues, the method will diverge for any
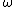 if the initial error
if the initial error 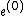 has nonzero components in the corresponding eigenvectors.
has nonzero components in the corresponding eigenvectors.
