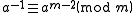Modular multiplicative inverse
Encyclopedia
The modular multiplicative inverse of an integer
a modulo
m is an integer x such that
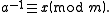
That is, it is the multiplicative inverse
in the ring
of integers modulo m. This is equivalent to
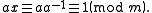
The multiplicative inverse of a modulo m exists if and only if
a and m are coprime
(i.e., if gcd(a, m) = 1). If the modular multiplicative inverse of a modulo m exists, the operation of division
by a modulo m can be defined as multiplying by the inverse, which is in essence the same concept as division in the field
of reals.
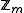where m is the modulus. Therefore, the x that is selected as the modular multiplicative inverse is generally a member of 
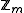for most applications.
For example,
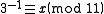
yields
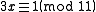
The smallest x that solves this congruence is 4; therefore, the modular multiplicative inverse of 3 (mod 11) is 4. However, another x that solves the congruence is 15 (easily found by adding m, which is 11, to the found inverse).
. The algorithm finds solutions to Bézout's identity
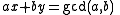
where a, b are given and x, y, and gcd(a, b) are the integers that the algorithm discovers. So, since the modular multiplicative inverse is the solution to
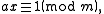
by the definition of congruence, m | ax − 1, which means that m is a divisor
of ax − 1. This, in turn, means that
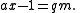
Rearranging produces
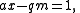
with a and m given, x the inverse, and q an integer multiple that will be discarded. This is the exact form of equation that the extended Euclidean algorithm solves—the only difference being that gcd(a, m) = 1 is predetermined instead of discovered. Thus, a needs to be coprime
to the modulus, or the inverse won't exist. The inverse is x, and q is discarded.
This algorithm runs in time O(log(m)2), assuming |a| < m, and is generally more efficient than exponentiation.
According to Euler's theorem, if a is coprime
to m, that is, gcd
(a, m) = 1, then
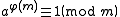
where φ(m) is Euler's totient function
. This follows from the fact that a belongs to the multiplicative group
(Z/mZ)* iff
a is coprime
to m. Therefore the modular multiplicative inverse can be found directly:
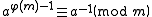
In the special case when m is a prime, the modular inverse is given by the above equation as:
This method is generally slower than the extended Euclidean algorithm, but is sometimes used when an implementation for modular exponentiation is already available. Some disadvantages of this method include:
. Factorization is widely believed to be a mathematically hard problem. However, calculating φ(m) is trivial in some common cases such as when m is known to be prime or a power of a prime.exponentiation. Though it can be implemented more efficiently using modular exponentiation
, when large values of m are involved this is most efficiently computed with the Montgomery reduction
method. This algorithm itself requires a modular inverse mod m, which is what we wanted to calculate in the first place. Without the Montgomery method, we're left with standard binary exponentiation which requires division mod m at every step, a slow operation when m is large. Furthermore, any kind of modular exponentiation is a taxing operation with computational complexity O
(log
φ(m)) = O(log m).
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
a modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
m is an integer x such that
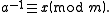
That is, it is the multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers modulo m. This is equivalent to
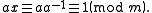
The multiplicative inverse of a modulo m exists if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
a and m are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
(i.e., if gcd(a, m) = 1). If the modular multiplicative inverse of a modulo m exists, the operation of division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
by a modulo m can be defined as multiplying by the inverse, which is in essence the same concept as division in the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of reals.
Explanation
When the inverse exists, it is always unique in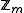 where m is the modulus. Therefore, the x that is selected as the modular multiplicative inverse is generally a member of 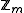for most applications.For example,
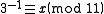
yields
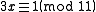
The smallest x that solves this congruence is 4; therefore, the modular multiplicative inverse of 3 (mod 11) is 4. However, another x that solves the congruence is 15 (easily found by adding m, which is 11, to the found inverse).
Extended Euclidean algorithm
The modular multiplicative inverse of a modulo m can be found with the extended Euclidean algorithmExtended Euclidean algorithm
The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. The algorithm finds solutions to Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
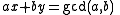
where a, b are given and x, y, and gcd(a, b) are the integers that the algorithm discovers. So, since the modular multiplicative inverse is the solution to
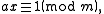
by the definition of congruence, m | ax − 1, which means that m is a divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of ax − 1. This, in turn, means that
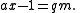
Rearranging produces
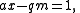
with a and m given, x the inverse, and q an integer multiple that will be discarded. This is the exact form of equation that the extended Euclidean algorithm solves—the only difference being that gcd(a, m) = 1 is predetermined instead of discovered. Thus, a needs to be coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to the modulus, or the inverse won't exist. The inverse is x, and q is discarded.
This algorithm runs in time O(log(m)2), assuming |a| < m, and is generally more efficient than exponentiation.
Using Euler's theorem
As an alternative to the extended Euclidean algorithm, Euler's theorem may be used to compute modular inverse:According to Euler's theorem, if a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to m, that is, gcd
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(a, m) = 1, then
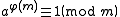
where φ(m) is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
. This follows from the fact that a belongs to the multiplicative group
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
(Z/mZ)* iff
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to m. Therefore the modular multiplicative inverse can be found directly:
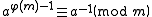
In the special case when m is a prime, the modular inverse is given by the above equation as:
This method is generally slower than the extended Euclidean algorithm, but is sometimes used when an implementation for modular exponentiation is already available. Some disadvantages of this method include:
- the required knowledge of φ(
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
. Factorization is widely believed to be a mathematically hard problem. However, calculating φ(m) is trivial in some common cases such as when m is known to be prime or a power of a prime.
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
, when large values of m are involved this is most efficiently computed with the Montgomery reduction
Montgomery reduction
In arithmetic computation, Montgomery reduction is an algorithm introduced in 1985 by Peter Montgomery that allows modular arithmetic to be performed efficiently when the modulus is large ....
method. This algorithm itself requires a modular inverse mod m, which is what we wanted to calculate in the first place. Without the Montgomery method, we're left with standard binary exponentiation which requires division mod m at every step, a slow operation when m is large. Furthermore, any kind of modular exponentiation is a taxing operation with computational complexity O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(log
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
φ(m)) = O(log m).
See also
- Inversive congruential generatorInversive congruential generatorInversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
- Modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
- Number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
- Public-key cryptographyPublic-key cryptographyPublic-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...