Modulational instability
Encyclopedia
In the field of nonlinear optics
, modulational instability is a phenomenon whereby deviations from an optical waveform are reinforced by nonlinearity, leading to the generation of spectral
-sidebands and the eventual breakup of the waveform into a train of pulses.
than pulses with longer wavelength. (This condition assumes a focussing Kerr nonlinearity, whereby refractive index increases with optical intensity.) There is also a threshold power, below which no instability will be seen.
The instability is strongly dependent on the frequency of the perturbation. At certain frequencies, a perturbation will have little effect, whilst at other frequencies, a perturbation will grow exponentially
. The overall gain
spectrum can be derived analytically
, as is shown below. Random perturbations will generally contain a broad range of frequency components, and so will cause the generation of spectral sidebands which reflect the underlying gain spectrum.
The tendency of a perturbing signal to grow makes modulation instability a form of amplification
. By tuning an input signal to a peak of the gain spectrum, it is possible to create an optical amplifier
.
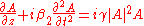
which describes the evolution of a slowly varying envelope
with time 
and distance of propagation 
. The model includes group velocity dispersion described by the parameter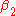 
, and Kerr nonlinearity with magnitude 
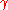. A waveform of constant power 
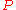is assumed. This is given by the solution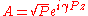
where the oscillatory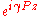
phase factor accounts for the difference between the linear refractive index
, and the modified refractive index, as raised by the Kerr effect. The beginning of instability can be investigated by perturbing this solution as
where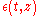
is the perturbation term (which, for mathematical convenience, has been multiplied by the same phase factor as 
). Substituting this back into the Nonlinear Schrödinger equation gives a perturbation equation
of the form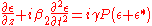
where the perturbation has been assumed to be small, such that
. Instability can now be discovered by searching for solutions of the perturbation equation which grow exponentially. This can be done using a trial function of the general form
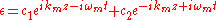
where
and 
are the frequency
and wavenumber
of a perturbation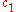, and
and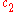 
are constants. The Nonlinear Schrödinger equation is constructed by removing the carrier wave
of the light being modelled, and so the frequency of the light being perturbed is formally zero. Therefore
and 
don't represent absolute frequencies and wavenumbers, but the difference between these and those of the initial beam of light. It can be shown that the trial function is valid, subject to the condition
This dispersion relation is vitally dependent on the sign of the term within the square root, as if positive, the wavenumber will be real
, corresponding to mere oscillation
s around the unperturbed solution, whilst if negative, the wavenumber will become imaginary
, corresponding to exponential growth and thus instability. Therefore, instability will occur when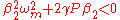
This condition describes both the requirement for anomalous dispersion (such that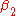
is negative) and the requirement that a threshold power be exceeded. The gain spectrum can be described by defining a gain parameter as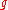 
, so that the power of a perturbing signal grows with distance as 
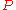
. The gain is therefore given by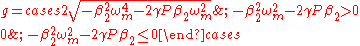
where as noted above,
is the difference between the frequency of the perturbation and the frequency of the initial light.
Nonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
, modulational instability is a phenomenon whereby deviations from an optical waveform are reinforced by nonlinearity, leading to the generation of spectral
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
-sidebands and the eventual breakup of the waveform into a train of pulses.
Initial instability and gain
Modulation instability only happens under certain circumstances. The most important condition is anomalous group velocity dispersion, whereby pulses with shorter wavelengths travel with higher group velocityGroup velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
than pulses with longer wavelength. (This condition assumes a focussing Kerr nonlinearity, whereby refractive index increases with optical intensity.) There is also a threshold power, below which no instability will be seen.
The instability is strongly dependent on the frequency of the perturbation. At certain frequencies, a perturbation will have little effect, whilst at other frequencies, a perturbation will grow exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
. The overall gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
spectrum can be derived analytically
Analytical expression
In mathematics, an analytical expression is a mathematical expression, constructed using well-known operations that lend themselves readily to calculation...
, as is shown below. Random perturbations will generally contain a broad range of frequency components, and so will cause the generation of spectral sidebands which reflect the underlying gain spectrum.
The tendency of a perturbing signal to grow makes modulation instability a form of amplification
Amplifier
Generally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
. By tuning an input signal to a peak of the gain spectrum, it is possible to create an optical amplifier
Optical amplifier
An optical amplifier is a device that amplifies an optical signal directly, without the need to first convert it to an electrical signal. An optical amplifier may be thought of as a laser without an optical cavity, or one in which feedback from the cavity is suppressed...
.
Mathematical derivation of gain spectrum
The gain spectrum can be derived by starting with a model of modulation instability based upon the Nonlinear Schrödinger equationNonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
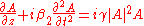
which describes the evolution of a slowly varying envelope
Slowly varying envelope approximation
In physics, the slowly varying envelope approximation is the assumption that the envelope of a forward-travelling wave pulse varies slowly in time and space compared to a period or wavelength...
with time and distance of propagation . The model includes group velocity dispersion described by the parameter 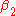, and Kerr nonlinearity with magnitude 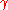. A waveform of constant power 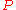is assumed. This is given by the solution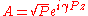where the oscillatory
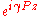phase factor accounts for the difference between the linear refractive indexRefractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
, and the modified refractive index, as raised by the Kerr effect. The beginning of instability can be investigated by perturbing this solution as
where
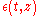is the perturbation term (which, for mathematical convenience, has been multiplied by the same phase factor as ). Substituting this back into the Nonlinear Schrödinger equation gives a perturbation equationPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of the form
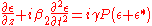
where the perturbation has been assumed to be small, such that
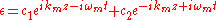
. Instability can now be discovered by searching for solutions of the perturbation equation which grow exponentially. This can be done using a trial function of the general formwhere
and are the frequencyFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
of a perturbation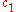, and
and 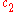are constants. The Nonlinear Schrödinger equation is constructed by removing the carrier waveCarrier wave
In telecommunications, a carrier wave or carrier is a waveform that is modulated with an input signal for the purpose of conveying information. This carrier wave is usually a much higher frequency than the input signal...
of the light being modelled, and so the frequency of the light being perturbed is formally zero. Therefore
and don't represent absolute frequencies and wavenumbers, but the difference between these and those of the initial beam of light. It can be shown that the trial function is valid, subject to the conditionThis dispersion relation is vitally dependent on the sign of the term within the square root, as if positive, the wavenumber will be real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, corresponding to mere oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s around the unperturbed solution, whilst if negative, the wavenumber will become imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, corresponding to exponential growth and thus instability. Therefore, instability will occur when
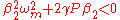
This condition describes both the requirement for anomalous dispersion (such that
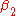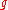
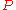
is negative) and the requirement that a threshold power be exceeded. The gain spectrum can be described by defining a gain parameter as , so that the power of a perturbing signal grows with distance as . The gain is therefore given by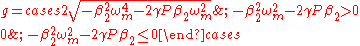where as noted above,
is the difference between the frequency of the perturbation and the frequency of the initial light.