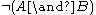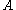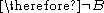Modus ponendo tollens is a valid rule of inference

Rule of inference

In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...

, sometimes abbreviated MPT. It is closely related to Modus ponens

Modus ponens

In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...

 and modus tollens

Modus tollens

In classical logic, modus tollens has the following argument form:- Formal notation :...

. It is usually described as having the form:

1. Not both A and B
2. A
3. Therefore, not B

For example:

1. Ann and Bill cannot both win the race.
2. Ann will win the race.
3. Therefore, Bill cannot win the race.

As E.J. Lemmon describes it:"Modus ponendo tollens is the principle that, if the negation of a conjunction holds and also one of its conjuncts, then the negation of its other conjunct holds."

In logic notation

Table of logic symbols

In logic, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related...

this can be represented as:

1. 
2. 
3.