
Table of logic symbols
Encyclopedia
In logic
, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related field of mathematics. Additionally, the third column contains an informal definition, and the fourth column gives a short example.
Be aware that, outside of logic, different symbols have the same meaning, and the same symbol has, depending on the context, different meanings.
, an outdated way for denoting AND, still in use in electronics; for example "A·B" is the same as "A&B"
, used as abbreviation for standard numerals. For example, using HTML style "" is a shorthand for the standard numeral "SSSS0".
or : Sheffer stroke
, the sign for the NAND operator.: strike out existential quantifier same as "¬∃": is a model
of: is true of: negated ⊢, the sign for "does not prove", for example T ⊬ P says "P is not a theorem of T": is not true of: another NAND operator, can also be rendered as ∧: another NOR operator, can also be rendered as V: modal operator for "it is possible that", "it is not necessarily not" or rarely "it is not provable not" (in most modal logics it is defined as "¬◻¬"): usually used for ad-hoc operators or : Webb-operator or Peirce arrow, the sign for NOR
. Confusingly, "⊥" is also the sign for contradiction or absurdity.
and : corner quotes, also called "Quine quotes"; the standard symbol used for denoting Gödel number
; for example "⌜G⌝" denotes the Gödel number of G. (Typographical note: although the quotes appears as a "pair" in unicode (231C and 231D), they are not symmetrical in some fonts. And in some fonts (for example Arial) they are only symmetrical in certain sizes. Alternatively the quotes can be rendered as ⌈ and ⌉ (U+2308 and U+2309) or by using a negation symbol and a reversed negation symbol ⌐ ¬ in superscript mode. )
or : modal operator for "it is necessary that" (in modal logic
), or "it is provable that" (in provability logic
), or "it is obligatory that" (in deontic logic
), or "it is believed that" (in doxastic logic).
Note that the following operators are rarely supported by natively installed fonts. If you wish to use these in a web page, you should always embed the necessary fonts so the page viewer can see the web page without having the necessary fonts installed in their computer.: modal operator for was never: modal operator for will never be: modal operator for was always: modal operator for will always be: sometimes used for "relation", also used for denoting various ad hoc relations (for example, for denoting "witnessing" in the context of Rosser's trick
) See here for an image of glyph. Added to Unicode 3.2.0.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related field of mathematics. Additionally, the third column contains an informal definition, and the fourth column gives a short example.
Be aware that, outside of logic, different symbols have the same meaning, and the same symbol has, depending on the context, different meanings.
Basic logic symbols
| Name | Explanation | Examples | Unicode Value |
HTML Entity |
LaTeX LaTeX LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to... symbol |
|
|---|---|---|---|---|---|---|
| Should be read as | ||||||
| Category | ||||||
→ ⊃ |
material implication | A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. → may mean the same as ⇒ (the symbol may also indicate the domain and codomain of a function Function (mathematics) In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can... ; see table of mathematical symbols Table of mathematical symbols This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:... ). ⊃ may mean the same as ⇒ (the symbol may also mean superset SuperSet SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst... ). |
x = 2 ⇒ x2 = 4 is true, but x2 = 4 ⇒ x = 2 is in general false (since x could be −2). | U+21D2 U+2192 U+2283 |
⇒ → ⊃ |
 \to \to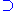 \supset \supset |
| implies; if .. then | ||||||
| propositional logic, Heyting algebra Heyting algebra In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b... |
||||||
≡ ↔ |
material equivalence | A ⇔ B means A is true if and only if B is true. | x + 5 = y +2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 |
⇔ ≡ ↔ |
 \equiv \equiv \leftrightarrow \leftrightarrow |
| if and only if; iff | ||||||
| propositional logic | ||||||
˜ ! |
negation Negation In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified... |
The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front. |
¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) |
U+00AC U+02DC |
¬ ˜ ~ |
 \sim \sim |
| not | ||||||
| propositional logic | ||||||
• & |
logical conjunction Logical conjunction In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false.... |
The statement A ∧ B is true if A and B are both true; else it is false. | n < 4 ∧ n >2 ⇔ n = 3 when n is a natural number Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... . |
U+2227 U+0026 |
∧ & |
 \wedge or \land \wedge or \land\& |
| and | ||||||
| propositional logic | ||||||
+ ǀǀ |
logical disjunction Logical disjunction In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are... |
The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... . |
U+2228 | ∨ | 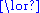 \lor \lor |
| or | ||||||
| propositional logic | ||||||
| exclusive disjunction | The statement A ⊕ B is true when either A or B, but not both, are true. A B means the same. | (¬A) ⊕ A is always true, A ⊕ A is always false. | U+2295 U+22BB |
⊕ |  \oplus \oplus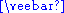 \veebar \veebar |
|
| xor | ||||||
| propositional logic, Boolean algebra | ||||||
T 1 |
Tautology Tautology (logic) In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense... |
The statement ⊤ is unconditionally true. | A ⇒ ⊤ is always true. | U+22A4 | T |  \top \top |
| top | ||||||
| propositional logic, Boolean algebra | ||||||
F 0 |
Contradiction Contradiction In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other... |
The statement ⊥ is unconditionally false. | ⊥ ⇒ A is always true. | U+22A5 | ⊥ F |
 \bot \bot |
| bottom | ||||||
| propositional logic, Boolean algebra | ||||||
| universal quantification Universal quantification In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing.... |
∀ x: P(x) means P(x) is true for all x. | ∀ n ∈ N: n2 ≥ n. | U+2200 | ∀ |  \forall \forall |
|
| for all; for any; for each | ||||||
| predicate logic Predicate logic In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified... |
||||||
| existential quantification Existential quantification In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier... |
∃ x: P(x) means there is at least one x such that P(x) is true. | ∃ n ∈ N: n is even. | U+2203 | ∃ |  \exists \exists |
|
| there exists | ||||||
| first-order logic First-order logic First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic... |
||||||
| uniqueness quantification Uniqueness quantification In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is... |
∃! x: P(x) means there is exactly one x such that P(x) is true. | ∃! n ∈ N: n + 5 = 2n. | U+2203 U+0021 | ∃ |  \exists \exists |
|
| there exists exactly one | ||||||
| first-order logic First-order logic First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic... |
||||||
≡ :⇔ |
definition Definition A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings... |
x := y or x ≡ y means x is defined to be another name for y (but note that ≡ can also mean other things, such as congruence Congruence relation In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure... ). P :⇔ Q means P is defined to be logically equivalent Logical equivalence In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other... to Q. |
cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) |
U+2254 (U+003A U+003D) U+2261 U+003A U+229C |
:= : ≡ ⇔ |
 \equiv \equiv \Leftrightarrow \Leftrightarrow |
| is defined as | ||||||
| everywhere | ||||||
| precedence grouping | Perform the operations inside the parentheses first. | (8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4. | U+0028 U+0029 |  |
||
| everywhere | ||||||
| turnstile Turnstile A turnstile, also called a baffle gate, is a form of gate which allows one person to pass at a time. It can also be made so as to enforce one-way traffic of people, and in addition, it can restrict passage only to people who insert a coin, a ticket, a pass, or similar... |
x y means y is provable from x (in some specified formal system). | A → B ¬B → ¬A | U+22A6 | &⊢ |  \vdash \vdash |
|
| provable | ||||||
| propositional logic, first-order logic First-order logic First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic... |
||||||
| double turnstile Double turnstile In logic, the symbol \vDash is called the double turnstile. It is closely related to the turnstile symbol, which has a single bar across the middle. It is often read as "models" or "is a semantic consequence of". In TeX, the turnstile symbol \vDash is obtained from the command \vDash... |
x ⊨ y means x semantically entails y | A → B ⊨ ¬B → ¬A | U+22A7 | ⊨ |  \models \models |
|
| entails | ||||||
| propositional logic, first-order logic First-order logic First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic... |
Advanced and rarely used logical symbols
These symbols are sorted by their Unicode value:, an outdated way for denoting AND, still in use in electronics; for example "A·B" is the same as "A&B"
- ·: Center dot with a line above it (using HTML style). Outdated way for denoting NAND, for example "A·B" is the same as "A NAND B" or "A|B" or "¬(A & B)". See also Unicode .
, used as abbreviation for standard numerals. For example, using HTML style "" is a shorthand for the standard numeral "SSSS0".
- Overline, is also a rarely used format for denoting Gödel numbers, for example "AVB" says the Gödel number of "(AVB)"
- Overline is also an outdated way for denoting negation, still in use in electronics; for example "AVB" is the same as "¬(AVB)"
or : Sheffer stroke
Sheffer stroke
In Boolean functions and propositional calculus, the Sheffer stroke, named after Henry M. Sheffer, written "|" , "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both"...
, the sign for the NAND operator.: strike out existential quantifier same as "¬∃": is a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of: is true of: negated ⊢, the sign for "does not prove", for example T ⊬ P says "P is not a theorem of T": is not true of: another NAND operator, can also be rendered as ∧: another NOR operator, can also be rendered as V: modal operator for "it is possible that", "it is not necessarily not" or rarely "it is not provable not" (in most modal logics it is defined as "¬◻¬"): usually used for ad-hoc operators or : Webb-operator or Peirce arrow, the sign for NOR
Logical NOR
In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false...
. Confusingly, "⊥" is also the sign for contradiction or absurdity.
and : corner quotes, also called "Quine quotes"; the standard symbol used for denoting Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
; for example "⌜G⌝" denotes the Gödel number of G. (Typographical note: although the quotes appears as a "pair" in unicode (231C and 231D), they are not symmetrical in some fonts. And in some fonts (for example Arial) they are only symmetrical in certain sizes. Alternatively the quotes can be rendered as ⌈ and ⌉ (U+2308 and U+2309) or by using a negation symbol and a reversed negation symbol ⌐ ¬ in superscript mode. )
or : modal operator for "it is necessary that" (in modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
), or "it is provable that" (in provability logic
Provability logic
Provability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic....
), or "it is obligatory that" (in deontic logic
Deontic logic
Deontic logic is the field of logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts...
), or "it is believed that" (in doxastic logic).
Note that the following operators are rarely supported by natively installed fonts. If you wish to use these in a web page, you should always embed the necessary fonts so the page viewer can see the web page without having the necessary fonts installed in their computer.: modal operator for was never: modal operator for will never be: modal operator for was always: modal operator for will always be: sometimes used for "relation", also used for denoting various ad hoc relations (for example, for denoting "witnessing" in the context of Rosser's trick
Rosser's trick
In mathematical logic, Rosser's trick is a method for proving Gödel's incompleteness theorems without the assumption that the theory being considered is ω-consistent . This method was introduced by J...
) See here for an image of glyph. Added to Unicode 3.2.0.
See also
- Table of mathematical symbolsTable of mathematical symbolsThis is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
- Polish notation
- Logic AlphabetLogic alphabetThe logic alphabet constitutes an iconic set of symbols that systematically represents the sixteen possible binary truth functions of logic. The logic alphabet was developed by Dr. Shea Zellweger. Dr. Zellweger, now retired, was Chair of the Psychology Department for Mount Union College and served...
, a suggested set of logical symbols. - Unicode Mathematical OperatorsUnicode Mathematical OperatorsUnicode ranges mathematical operators and symbols in multiple blocks.* Mathematical Operators * Miscellaneous Mathematical Symbols-A * Miscellaneous Mathematical Symbols-B...
External links
- Named character entities in HTMLHTMLHyperText Markup Language is the predominant markup language for web pages. HTML elements are the basic building-blocks of webpages....
4.0.

