Heyting algebra
Encyclopedia
In mathematics
, a Heyting algebra, named after Arend Heyting
, is a bounded lattice equipped with a binary operation a→b of implication such that (a→b)∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b. From a logical standpoint, A→B is by this definition the weakest proposition for which modus ponens
, the inference rule A→B, A ⊢ B, is sound. Equivalently a Heyting algebra is a residuated lattice
whose monoid operation a•b is a∧b; yet another definition is as a posetal
cartesian closed category
with all finite sums. Like Boolean algebra
s, Heyting algebras form a variety
axiomatizable with finitely many equations.
As lattices, Heyting algebras can be shown to be distributive
. Every Boolean algebra is a Heyting algebra when a→b is defined as usual as ¬a∨b, as is every complete distributive lattice when a→b is taken to be the supremum
of the set of all c for which a∧c ≤ b. The open set
s of a topological space
form a complete distributive lattice and hence a Heyting algebra. In the finite case every nonempty distributive lattice, in particular every nonempty finite chain, is automatically bounded and complete and hence a Heyting algebra.
It follows from the definition that 1 ≤ 0→a, corresponding to the intuition that any proposition a is implied by a contradiction 0. Although the negation operation ¬a is not part of the definition, it is definable as a→0. The definition implies that a∧¬a = 0, making the intuitive content of ¬a the proposition that to assume a would lead to a contradiction, from which any other proposition would then follow. It can further be shown that a ≤ ¬¬a, although the converse, ¬¬a ≤ a, is not true in general, that is, double negation
does not hold in general in a Heyting algebra.
Heyting algebras generalize Boolean algebras in the sense that a Heyting algebra satisfying a∨¬a = 1 (excluded middle), equivalently ¬¬a = a (double negation
), is a Boolean algebra. Those elements of a Heyting algebra of the form ¬a comprise a Boolean lattice, but in general this is not a subalgebra
of H (see below).
Heyting algebras serve as the algebraic models of propositional intuitionistic logic
in the same way Boolean algebra
s model propositional classical logic
. Complete Heyting algebra
s are a central object of study in pointless topology
. The internal logic of an elementary topos is based on the Heyting algebra of subobject
s of the terminal object 1 ordered by inclusion, equivalently the morphisms from 1 to the subobject classifier
Ω.
Every Heyting algebra with exactly one coatom is subdirectly irreducible, whence every Heyting algebra can be made an SI
by adjoining a new top. It follows that even among the finite Heyting algebras there exist infinitely many that are subdirectly irreducible, no two of which have the same equational theory. Hence no finite set of finite Heyting algebras can supply all the counterexamples to non-laws of Heyting algebra. This is in sharp contrast to Boolean algebras, whose only SI is the two-element one, which on its own therefore suffices for all counterexamples to non-laws of Boolean algebra, the basis for the simple truth table
decision method. Nevertheless it is decidable whether an equation holds of all Heyting algebras.
Heyting algebras are less often called pseudo-Boolean algebras, or even Brouwer lattices, although the latter term may denote the dual definition, or have a slightly more general meaning.
is a bounded lattice such that for all 
and 
in 
there is a greatest element 
of 
such that
This element is the relative pseudo-complement of
with respect to 
, and is denoted 
. We write 1 and 0 for the largest and the smallest element of 
, respectively.
In any Heyting algebra, one defines the pseudo-complement
of any element 
by setting 
. By definition, 
, and 
is the largest element having this property. However, it is not in general true that 
, thus 
is only a pseudo-complement, not a true complement
, as would be the case in a Boolean algebra.
A complete Heyting algebra
is a Heyting algebra that is a complete lattice
.
A subalgebra of a Heyting algebra
is a subset 
of 
containing 0 and 1 and closed under the operations 
and 
. It follows that it is also closed under 
. A subalgebra is made into a Heyting algebra by the induced operations.
for some fixed
in 
. A bounded lattice 
is a Heyting algebra if and only if
all mappings
are the lower adjoint of a monotone Galois connection
. In this case the respective upper adjoints
are given by 
, where 
is defined as above.
Yet another definition is as a residuated lattice
whose monoid operation is
. The monoid unit must then be the top element 1. Commutativity of this monoid implies that the two residuals coincide as 
.
with largest and smallest elements 1 and 0, and a binary operation 
, these together form a Heyting algebra if and only if the following hold:
where 4 is the distributive law for
.
Given a set
with three binary operations 
and 
, and two distinguished elements 0 and 1, then 
is a Heyting algebra for these operations (and the relation 
defined by the condition that 
when 
) if and only if the following conditions hold for any elements 
and 
of 
:
Finally, we define
to be 
.
Condition 1 says that equivalent formulas should be identified. Condition 2 says that provably true formulas are closed under modus ponens
. Conditions 3 and 4 are then conditions. Conditions 5, 6 and 7 are and conditions. Conditions 8, 9 and 10 are or conditions. Condition 11 is a false condition.
Of course, if a different set of axioms were chosen for logic, we could modify ours accordingly.
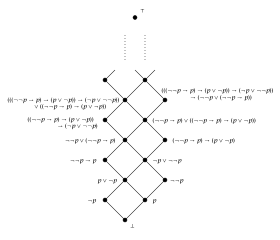
Notice that falsifies the law of excluded middle.
on a Heyting algebra 
can be recovered from the operation 
as follows: for any elements 
of 
, 
if and only if 
.
In contrast to some many-valued logics, Heyting algebras share the following property with Boolean algebras: if negation has a fixed point
(i.e.
for some 
), then the Heyting algebra is the trivial one-element Heyting algebra.
of propositional calculus (using, in addition to the variables, the connectives 
, and the constants 0 and 1), it is a fact, proved early on in any study of Heyting algebras, that the following two conditions are equivalent:
The implication
is extremely useful and is the principal practical method for proving identities in Heyting algebras. In practice, one frequently uses the deduction theorem
in such proofs.
Since for any
and 
in a Heyting algebra 
we have 
if and only if 
, it follows from 
that whenever a formula 
is provably true, we have 
for any Heyting algebra 
, and any elements 
. (It follows from the deduction theorem that 
is provable [from nothing] if and only if 
is provable from 
, that is, if 
is a provable consequence of 
.) In particular, if 
and 
are provably equivalent, then 
, since 
is an order relation.
can be proved by examining the logical axioms of the system of proof and verifying that their value is 1 in any Heyting algebra, and then verifying that the application of the rules of inference to expressions with value 1 in a Heyting algebra results in expressions with value 1. For example, let us choose the system of proof having modus ponens
as its sole rule of inference, and whose axioms are the Hilbert-style ones given at Intuitionistic logic#Axiomatization. Then the facts to be verified follow immediately from the axiom-like definition of Heyting algebras given above.
also provides a method for proving that certain propositional formulas, though tautologies
in classical logic, cannot be proved in intuitionist propositional logic. In order to prove that some formula
is not provable, it is enough to exhibit a Heyting algebra 
and elements 
such that 
.
If one wishes to avoid mention of logic, then in practice it becomes necessary to prove as a lemma a version of the deduction theorem valid for Heyting algebras: for any elements
and 
of a Heyting algebra 
, we have 
.
For more on the implication
, see the section "Universal constructions" below.
. Specifically, we always have the identities
The distributive law is sometimes stated as an axiom, but in fact it follows from the existence of relative pseudo-complements. The reason is that, being the lower adjoint of a Galois connection
,
preserves
all existing suprema. Distributivity in turn is just the preservation of binary suprema by
.
By a similar argument, the following infinite distributive law holds in any complete Heyting algebra:
for any element
in 
and any subset 
of 
. Conversely, any complete lattice satisfying the above infinite distributive law is a complete Heyting algebra, with
being its relative pseudo-complement operation.
The equivalence of these conditions can be restated simply as the identity
, valid for all 
.
Elements
and 
of a Heyting algebra 
are called complements to each other if 
and 
. If it exists, any such 
is unique and must in fact be equal to 
. We call an element 
complemented if it admits a complement. It is true that if 
is complemented, then so is 
, and then 
and 
are complements to each other. However, confusingly, even if 
is not complemented, 
may nonetheless have a complement (not equal to 
). In any Heyting algebra, the elements 0 and 1 are complements to each other. For instance, it is possible that 
is 0 for every 
different from 0, and 1 if 
, in which case 0 and 1 are the only regular elements.
Any complemented element of a Heyting algebra is regular, though the converse is not true in general. In particular, 0 and 1 are always regular.
For any Heyting algebra H, the following conditions are equivalent:
In this case, the element is equal to
The regular (resp. complemented) elements of any Heyting algebra H constitute a Boolean algebra Hreg (resp. Hcomp), in which the operations ∧, ¬ and →, as well as the constants 0 and 1, coincide with those of H. In the case of Hcomp, the operation ∨ is also the same, hence Hcomp is a subalgebra of H. In general however, Hreg will not be a subalgebra of H, because its join operation ∨reg may be differ from ∨. For we have See below for necessary and sufficient conditions in order for ∨reg to coincide with ∨.
, for all 
.
However, the other De Morgan law does not always hold. We have instead a weak de Morgan law:
, for all 
.
The following statements are equivalent for all Heyting algebras H:
Condition 2 is the other De Morgan law. Condition 6 says that the join operation ∨reg on the Boolean algebra Hreg of regular elements of H coincides with the operation ∨ of H. Condition 7 states that every regular element is complemented, i.e., Hreg = Hcomp.
We prove the equivalence. Clearly and are trivial. Furthermore, and result simply from the first De Morgan law and the definition of regular elements. We show that by taking ¬x and ¬¬x in place of x and y in 6 and using the identity Notice that follows from the first De Morgan law, and results from the fact that the join operation ∨ on the subalgebra Hcomp is just the restriction of ∨ to Hcomp, taking into account the characterizations we have given of conditions 6 and 7. The implication is a trivial consequence of the weak De Morgan law, taking ¬x and ¬y in place of x and y in 5.
Heyting algebras satisfying the above properties are related to De Morgan logic
in the same way Heyting algebras in general are related to intuitionist logic.
of Heyting algebras if, for any elements x and y in H1, we have:
We put condition 6 in brackets because it follows from the others, as ¬x is just x→0, and one may or may not wish to consider ¬ to be a basic operation.
It follows from conditions 3 and 5 (or 1 alone, or 2 alone) that f is an increasing function, that is, that whenever .
Assume H1 and H2 are structures with operations →, ∧, ∨ (and possibly ¬) and constants 0 and 1, and f is a surjective mapping from H1 to H2 with properties 1 through 5 (or 1 through 6) above. Then if H1 is a Heyting algebra, so too is H2. This follows from the characterization of Heyting algebras as bounded lattices (thought of as algebraic structures rather than partially ordered sets) with an operation → satisfying certain identities.
.
For any Heyting algebra H, the map defines a morphism from H onto the Boolean algebra of its regular elements Hreg. This is not in general a morphism from H to itself, since the join operation of Hreg may be different from that of H.
The intersection of any set of filters on H is again a filter. Therefore, given any subset S of H there is a smallest filter containing S. We call it the filter generated by S. If S is empty, Otherwise, F is equal to the set of x in H such that there exist with
If H is a Heyting algebra and F is a filter on H, we define a relation ∼ on H as follows: we write whenever and both belong to F. Then ∼ is an equivalence relation
; we write for the quotient set. There is a unique Heyting algebra structure on such that the canonical surjection becomes a Heyting algebra morphism. We call the Heyting algebra the quotient of H by F.
Let S be a subset of a Heyting algebra H and let F be the filter generated by S. Then H/F satisfies the following universal property:
Let be a morphism of Heyting algebras. The kernel of ƒ, written ker ƒ, is the set It is a filter on H1. (Care should be taken because this definition, if applied to a morphism of Boolean algebras, is dual to what would be called the kernel of the morphism viewed as a morphism of rings.) By the foregoing, ƒ induces a morphism It is an isomorphism of onto the subalgebra ƒ[H1] of H2.
As always under the axiom-like definition of Heyting algebras, we define ≤ on H0 by the condition that x≤y if and only if x→y=1. Since, by the deduction theorem
, a formula F→G is provably true if and only if G is provable from F, it follows that [F]≤[G] if and only if F≼G. In other words, ≤ is the order relation on L/∼ induced by the preorder ≼ on L.
is not difficult to see, and its existence results essentially from the implication 1→2 of the section "Provable identities" above, in the form of its corollary that whenever F and G are provably equivalent formulas, F(〈ai〉)=G(〈ai〉) for any family of elements 〈ai〉in H.
The Heyting algebra HT that we have just defined can be viewed as a quotient of the free Heyting algebra H0 on the same set of variables, by applying the universal property of H0 with respect to HT, and the family of its elements 〈[Ai]〉.
Every Heyting algebra is isomorphic to one of the form HT. To see this, let H be any Heyting algebra, and let 〈ai: i∈I〉 be a family of elements generating H (for example, any surjective family). Now consider the set T of formulas J(〈Ai〉) in the variables 〈Ai: i∈I〉 such that J(〈ai〉)=1. Then we obtain a morphism f:HT→H by the universal property of HT, which is clearly surjective. It is not difficult to show that f is injective.
is, by definition of the pseudo-complement, the largest element x such that 
. This inequation is satisfied for any x, so the largest such x is 1.
Furthermore the rule of modus ponens
allows us to derive the formula Q from the formulas P and P → Q. But in any Heyting algebra, if P has the value 1, and P → Q has the value 1, then it means that
, and so 
; it can only be that Q has the value 1.
This means that if a formula is deducible from the laws of intuitionistic logic, being derived from its axioms by way of the rule of modus ponens, then it will always have the value 1 in all Heyting algebras under any assignment of values to the formula's variables. However one can construct a Heyting algebra in which the value of Peirce's law is not always 1. Consider the 3-element algebra {0,½,1} as given above. If we assign ½ to P and 0 to Q, then the value of Peirce's law ((P → Q) → P) → P is ½. It follows that Peirce's law cannot be intuitionistically derived. See Curry–Howard isomorphism for the general context of what this implies in type theory
.
The converse can be proven as well: if a formula always has the value 1, then it is deducible from the laws of intuitionistic logic, so the intuitionistically valid formulas are exactly those that always have a value of 1. This is similar to the notion that classically valid formulas are those formulas that have a value of 1 in the two-element Boolean algebra under any possible assignment of true and false to the formula's variables — that is, they are formulas which are tautologies in the usual truth-table sense. A Heyting algebra, from the logical standpoint, is then a generalization of the usual system of truth values, and its largest element 1 is analogous to 'true'. The usual two-valued logic system is a special case of a Heyting algebra, and the smallest non-trivial one, in which the only elements of the algebra are 1 (true) and 0 (false).
of the problem was established by R. Statman in 1979, who showed it was PSPACE-complete and hence at least as hard as deciding equations of Boolean algebra (shown NP-complete in 1971 by S. Cook) and conjectured to be considerably harder. The elementary or first-order theory of Heyting algebras is undecidable. It remains open whether the universal Horn theory of Heyting algebras, or word problem
, is decidable. Apropos of the word problem it is known that Heyting algebras are not locally finite (no Heyting algebra generated by a finite nonempty set is finite), in contrast to Boolean algebras which are locally finite and whose word problem is decidable. It is unknown whether free complete Heyting algebras exist except in the case of a single generator where the free Heyting algebra on one generator is trivially completable by adjoining a new top.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Heyting algebra, named after Arend Heyting
Arend Heyting
Arend Heyting was a Dutch mathematician and logician. He was a student of Luitzen Egbertus Jan Brouwer at the University of Amsterdam, and did much to put intuitionistic logic on a footing where it could become part of mathematical logic...
, is a bounded lattice equipped with a binary operation a→b of implication such that (a→b)∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b. From a logical standpoint, A→B is by this definition the weakest proposition for which modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
, the inference rule A→B, A ⊢ B, is sound. Equivalently a Heyting algebra is a residuated lattice
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
whose monoid operation a•b is a∧b; yet another definition is as a posetal
Posetal category
In mathematics, a posetal category is a category whose homsets each contain at most one morphism. As such a posetal category amounts to a preordered set...
cartesian closed category
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
with all finite sums. Like Boolean algebra
Boolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
s, Heyting algebras form a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
axiomatizable with finitely many equations.
As lattices, Heyting algebras can be shown to be distributive
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
. Every Boolean algebra is a Heyting algebra when a→b is defined as usual as ¬a∨b, as is every complete distributive lattice when a→b is taken to be the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the set of all c for which a∧c ≤ b. The open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
form a complete distributive lattice and hence a Heyting algebra. In the finite case every nonempty distributive lattice, in particular every nonempty finite chain, is automatically bounded and complete and hence a Heyting algebra.
It follows from the definition that 1 ≤ 0→a, corresponding to the intuition that any proposition a is implied by a contradiction 0. Although the negation operation ¬a is not part of the definition, it is definable as a→0. The definition implies that a∧¬a = 0, making the intuitive content of ¬a the proposition that to assume a would lead to a contradiction, from which any other proposition would then follow. It can further be shown that a ≤ ¬¬a, although the converse, ¬¬a ≤ a, is not true in general, that is, double negation
Double negation
In the theory of logic, double negation is expressed by saying that a proposition A is identical to not , or by the formula A = ~~A. Like the Law of Excluded Middle, this principle when extended to an infinite collection of individuals is disallowed by Intuitionistic logic...
does not hold in general in a Heyting algebra.
Heyting algebras generalize Boolean algebras in the sense that a Heyting algebra satisfying a∨¬a = 1 (excluded middle), equivalently ¬¬a = a (double negation
Double negation
In the theory of logic, double negation is expressed by saying that a proposition A is identical to not , or by the formula A = ~~A. Like the Law of Excluded Middle, this principle when extended to an infinite collection of individuals is disallowed by Intuitionistic logic...
), is a Boolean algebra. Those elements of a Heyting algebra of the form ¬a comprise a Boolean lattice, but in general this is not a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of H (see below).
Heyting algebras serve as the algebraic models of propositional intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
in the same way Boolean algebra
Boolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
s model propositional classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
. Complete Heyting algebra
Complete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
s are a central object of study in pointless topology
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
. The internal logic of an elementary topos is based on the Heyting algebra of subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s of the terminal object 1 ordered by inclusion, equivalently the morphisms from 1 to the subobject classifier
Subobject classifier
In category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
Ω.
Every Heyting algebra with exactly one coatom is subdirectly irreducible, whence every Heyting algebra can be made an SI
Subdirect irreducible
In the branch of mathematics known as universal algebra , a subdirectly irreducible algebra is an algebra that cannot be factored as a subdirect product of "simpler" algebras...
by adjoining a new top. It follows that even among the finite Heyting algebras there exist infinitely many that are subdirectly irreducible, no two of which have the same equational theory. Hence no finite set of finite Heyting algebras can supply all the counterexamples to non-laws of Heyting algebra. This is in sharp contrast to Boolean algebras, whose only SI is the two-element one, which on its own therefore suffices for all counterexamples to non-laws of Boolean algebra, the basis for the simple truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
decision method. Nevertheless it is decidable whether an equation holds of all Heyting algebras.
Heyting algebras are less often called pseudo-Boolean algebras, or even Brouwer lattices, although the latter term may denote the dual definition, or have a slightly more general meaning.
Formal definition
A Heyting algebra is a bounded lattice such that for all and in there is a greatest element of such thatThis element is the relative pseudo-complement of
with respect to , and is denoted . We write 1 and 0 for the largest and the smallest element of , respectively.In any Heyting algebra, one defines the pseudo-complement
of any element by setting . By definition, , and is the largest element having this property. However, it is not in general true that , thus is only a pseudo-complement, not a true complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
, as would be the case in a Boolean algebra.
A complete Heyting algebra
Complete Heyting algebra
In mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
is a Heyting algebra that is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
.
A subalgebra of a Heyting algebra
is a subset of containing 0 and 1 and closed under the operations and . It follows that it is also closed under . A subalgebra is made into a Heyting algebra by the induced operations.Lattice-theoretic definitions
An equivalent definition of Heyting algebras can be given by considering the mappingsfor some fixed
in . A bounded lattice is a Heyting algebra if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
all mappings
are the lower adjoint of a monotone Galois connectionGalois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
. In this case the respective upper adjoints
are given by , where is defined as above.Yet another definition is as a residuated lattice
Residuated lattice
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
whose monoid operation is
. The monoid unit must then be the top element 1. Commutativity of this monoid implies that the two residuals coincide as .Bounded lattice with an implication operation
Given a bounded lattice with largest and smallest elements 1 and 0, and a binary operation , these together form a Heyting algebra if and only if the following hold:
where 4 is the distributive law for
.Characterization using the axioms of intuitionistic logic
This characterization of Heyting algebras makes the proof of the basic facts concerning the relationship between intuitionist propositional calculus and Heyting algebras immediate. (For these facts, see the sections "Provable identities" and "Universal constructions.") One should think of the element 1 as meaning, intuitively, "provably true." Compare with the axioms at Intuitionistic logic#Axiomatization.Given a set
with three binary operations and , and two distinguished elements 0 and 1, then is a Heyting algebra for these operations (and the relation defined by the condition that when ) if and only if the following conditions hold for any elements and of :
Finally, we define
to be .Condition 1 says that equivalent formulas should be identified. Condition 2 says that provably true formulas are closed under modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
. Conditions 3 and 4 are then conditions. Conditions 5, 6 and 7 are and conditions. Conditions 8, 9 and 10 are or conditions. Condition 11 is a false condition.
Of course, if a different set of axioms were chosen for logic, we could modify ours accordingly.
Examples
- Every Boolean algebra is a Heyting algebra, with
given by 
.
- Every totally ordered setTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
that is a bounded lattice is also a Heyting algebra, where
is equal to 
when 
, and 1 otherwise.
- The simplest Heyting algebra that is not already a Boolean algebra is the totally ordered set {0, ½, 1} with
defined as above, yielding the operations:
Notice that falsifies the law of excluded middle.
- Every topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
provides a complete Heyting algebra in the form of its open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
lattice. In this case, the element
is the interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of the union of
and 
, where 
denotes the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
. Not all complete Heyting algebras are of this form. These issues are studied in pointless topologyPointless topologyIn mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
, where complete Heyting algebras are also called frames or locales.
- The Lindenbaum algebra of propositional intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
is a Heyting algebra.
- The global elementGlobal elementIn category theory, a global element of an object A from a category is a morphismwhere 1 is a terminal object of the category. Roughly speaking, global elements are a generalization of the notion of “elements” from the category of sets, and they can be used to import set-theoretic...
s of the subobject classifierSubobject classifierIn category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
of an elementary topos form a Heyting algebra; it is the Heyting algebra of truth values of the intuitionistic higher-order logic induced by the topos.
General properties
The ordering on a Heyting algebra can be recovered from the operation as follows: for any elements of , if and only if .In contrast to some many-valued logics, Heyting algebras share the following property with Boolean algebras: if negation has a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
(i.e.
for some ), then the Heyting algebra is the trivial one-element Heyting algebra.Provable identities
Given a formula of propositional calculus (using, in addition to the variables, the connectives , and the constants 0 and 1), it is a fact, proved early on in any study of Heyting algebras, that the following two conditions are equivalent:
- The formula
is provably true in intuitionist propositional calculus. - The identity
is true for any Heyting algebra 
and any elements 
.
The implication
is extremely useful and is the principal practical method for proving identities in Heyting algebras. In practice, one frequently uses the deduction theoremDeduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
in such proofs.
Since for any
and in a Heyting algebra we have if and only if , it follows from that whenever a formula is provably true, we have for any Heyting algebra , and any elements . (It follows from the deduction theorem that is provable [from nothing] if and only if is provable from , that is, if is a provable consequence of .) In particular, if and are provably equivalent, then , since is an order relation. can be proved by examining the logical axioms of the system of proof and verifying that their value is 1 in any Heyting algebra, and then verifying that the application of the rules of inference to expressions with value 1 in a Heyting algebra results in expressions with value 1. For example, let us choose the system of proof having modus ponensModus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
as its sole rule of inference, and whose axioms are the Hilbert-style ones given at Intuitionistic logic#Axiomatization. Then the facts to be verified follow immediately from the axiom-like definition of Heyting algebras given above.
also provides a method for proving that certain propositional formulas, though tautologiesTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
in classical logic, cannot be proved in intuitionist propositional logic. In order to prove that some formula
is not provable, it is enough to exhibit a Heyting algebra and elements such that .If one wishes to avoid mention of logic, then in practice it becomes necessary to prove as a lemma a version of the deduction theorem valid for Heyting algebras: for any elements
and of a Heyting algebra , we have .For more on the implication
, see the section "Universal constructions" below.Distributivity
Heyting algebras are always distributiveDistributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
. Specifically, we always have the identities
The distributive law is sometimes stated as an axiom, but in fact it follows from the existence of relative pseudo-complements. The reason is that, being the lower adjoint of a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
,
preservesLimit-preserving function (order theory)
In the mathematical area of order theory, one often speaks about functions that preserve certain limits, i.e. certain suprema or infima. Roughly speaking, these functions map the supremum/infimum of a set to the supremum/infimum of the image of the set...
all existing suprema. Distributivity in turn is just the preservation of binary suprema by
.By a similar argument, the following infinite distributive law holds in any complete Heyting algebra:
for any element
in and any subset of . Conversely, any complete lattice satisfying the above infinite distributive law is a complete Heyting algebra, withbeing its relative pseudo-complement operation.
Regular and complemented elements
An element x of a Heyting algebra H is called regular if either of the following equivalent conditions hold:
The equivalence of these conditions can be restated simply as the identity
, valid for all .Elements
and of a Heyting algebra are called complements to each other if and . If it exists, any such is unique and must in fact be equal to . We call an element complemented if it admits a complement. It is true that if is complemented, then so is , and then and are complements to each other. However, confusingly, even if is not complemented, may nonetheless have a complement (not equal to ). In any Heyting algebra, the elements 0 and 1 are complements to each other. For instance, it is possible that is 0 for every different from 0, and 1 if , in which case 0 and 1 are the only regular elements.Any complemented element of a Heyting algebra is regular, though the converse is not true in general. In particular, 0 and 1 are always regular.
For any Heyting algebra H, the following conditions are equivalent:
- H is a Boolean algebra;
- every x in H is regular;
- every x in H is complemented.
In this case, the element is equal to
The regular (resp. complemented) elements of any Heyting algebra H constitute a Boolean algebra Hreg (resp. Hcomp), in which the operations ∧, ¬ and →, as well as the constants 0 and 1, coincide with those of H. In the case of Hcomp, the operation ∨ is also the same, hence Hcomp is a subalgebra of H. In general however, Hreg will not be a subalgebra of H, because its join operation ∨reg may be differ from ∨. For we have See below for necessary and sufficient conditions in order for ∨reg to coincide with ∨.
The De Morgan laws in a Heyting algebra
One of the two De Morgan laws is satisfied in every Heyting algebra, namely, for all .However, the other De Morgan law does not always hold. We have instead a weak de Morgan law:
, for all .The following statements are equivalent for all Heyting algebras H:
- H satisfies both De Morgan laws,
Condition 2 is the other De Morgan law. Condition 6 says that the join operation ∨reg on the Boolean algebra Hreg of regular elements of H coincides with the operation ∨ of H. Condition 7 states that every regular element is complemented, i.e., Hreg = Hcomp.
We prove the equivalence. Clearly and are trivial. Furthermore, and result simply from the first De Morgan law and the definition of regular elements. We show that by taking ¬x and ¬¬x in place of x and y in 6 and using the identity Notice that follows from the first De Morgan law, and results from the fact that the join operation ∨ on the subalgebra Hcomp is just the restriction of ∨ to Hcomp, taking into account the characterizations we have given of conditions 6 and 7. The implication is a trivial consequence of the weak De Morgan law, taking ¬x and ¬y in place of x and y in 5.
Heyting algebras satisfying the above properties are related to De Morgan logic
Intermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
in the same way Heyting algebras in general are related to intuitionist logic.
Definition
Given two Heyting algebras H1 and H2 and a mapping we say that ƒ is a morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
of Heyting algebras if, for any elements x and y in H1, we have:
We put condition 6 in brackets because it follows from the others, as ¬x is just x→0, and one may or may not wish to consider ¬ to be a basic operation.
It follows from conditions 3 and 5 (or 1 alone, or 2 alone) that f is an increasing function, that is, that whenever .
Assume H1 and H2 are structures with operations →, ∧, ∨ (and possibly ¬) and constants 0 and 1, and f is a surjective mapping from H1 to H2 with properties 1 through 5 (or 1 through 6) above. Then if H1 is a Heyting algebra, so too is H2. This follows from the characterization of Heyting algebras as bounded lattices (thought of as algebraic structures rather than partially ordered sets) with an operation → satisfying certain identities.
Properties
The identity map from any Heyting algebra to itself is a morphism, and the composite of any two morphisms ƒ and g is a morphism. Hence Heyting algebras form a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
Examples
Given a Heyting algebra H and any subalgebra H1, the inclusion mapping is a morphism.For any Heyting algebra H, the map defines a morphism from H onto the Boolean algebra of its regular elements Hreg. This is not in general a morphism from H to itself, since the join operation of Hreg may be different from that of H.
Quotients
Let H be a Heyting algebra, and let We call F a filter on H if it satisfies the following properties:
The intersection of any set of filters on H is again a filter. Therefore, given any subset S of H there is a smallest filter containing S. We call it the filter generated by S. If S is empty, Otherwise, F is equal to the set of x in H such that there exist with
If H is a Heyting algebra and F is a filter on H, we define a relation ∼ on H as follows: we write whenever and both belong to F. Then ∼ is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
; we write for the quotient set. There is a unique Heyting algebra structure on such that the canonical surjection becomes a Heyting algebra morphism. We call the Heyting algebra the quotient of H by F.
Let S be a subset of a Heyting algebra H and let F be the filter generated by S. Then H/F satisfies the following universal property:
- Given any morphism of Heyting algebras satisfying for every ƒ factors uniquely through the canonical surjection That is, there is a unique morphism satisfying The morphism ƒ′ is said to be induced by ƒ.
Let be a morphism of Heyting algebras. The kernel of ƒ, written ker ƒ, is the set It is a filter on H1. (Care should be taken because this definition, if applied to a morphism of Boolean algebras, is dual to what would be called the kernel of the morphism viewed as a morphism of rings.) By the foregoing, ƒ induces a morphism It is an isomorphism of onto the subalgebra ƒ[H1] of H2.
Heyting algebra of propositional formulas in n variables up to intuitionist equivalence
The implication 2→1 in the section "Provable identities" is proved by showing that the result of the following construction is itself a Heyting algebra:- Consider the set L of propositional formulas in the variables A1, A2,..., An.
- Endow L with a preorder ≼ by defining F≼G if G is an (intuitionist) logical consequence of F, that is, if G is provable from F. It is immediate that ≼ is a preorder.
- Consider the equivalence relation F∼G induced by the preorder F≼G. (It is defined by F∼G if and only if F≼G and G≼F. In fact, ∼ is the relation of (intuitionist) logical equivalence.)
- Let H0 be the quotient set L/∼. This will be the desired Heyting algebra.
- We write [F] for the equivalence class of a formula F. Operations →, ∧, ∨ and ¬ are defined in an obvious way on L. Verify that given formulas F and G, the equivalence classes [F→G], [F∧G], [F∨G] and [¬F] depend only on [F] and [G]. This defines operations →, ∧, ∨ and ¬ on the quotient set H0=L/∼. Further define 1 to be the class of provably true statements, and set 0=[⊥].
- Verify that H0, together with these operations, is a Heyting algebra. We do this using the axiom-like definition of Heyting algebras. H0 satisfies conditions THEN-1 through FALSE because all formulas of the given forms are axioms of intuitionist logic. MODUS-PONENS follows from the fact that if a formula ⊤→F is provably true, where ⊤ is provably true, then F is provably true (by application of the rule of inference modus ponens). Finally, EQUIV results from the fact that if F→G and G→F are both provably true, then F and G are provable from each other (by application of the rule of inference modus ponens), hence [F]=[G].
As always under the axiom-like definition of Heyting algebras, we define ≤ on H0 by the condition that x≤y if and only if x→y=1. Since, by the deduction theorem
Deduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
, a formula F→G is provably true if and only if G is provable from F, it follows that [F]≤[G] if and only if F≼G. In other words, ≤ is the order relation on L/∼ induced by the preorder ≼ on L.
Free Heyting algebra on an arbitrary set of generators
In fact, the preceding construction can be carried out for any set of variables {Ai: i∈I} (possibly infinite). One obtains in this way the free Heyting algebra on the variables {Ai}, which we will again denote by H0. It is free in the sense that given any Heyting algebra H given together with a family of its elements 〈ai: i∈I 〉, there is a unique morphism f:H0→H satisfying f([Ai])=ai. The uniqueness of fis not difficult to see, and its existence results essentially from the implication 1→2 of the section "Provable identities" above, in the form of its corollary that whenever F and G are provably equivalent formulas, F(〈ai〉)=G(〈ai〉) for any family of elements 〈ai〉in H.
Heyting algebra of formulas equivalent with respect to a theory T
Given a set of formulas T in the variables {Ai}, viewed as axioms, the same construction could have been carried out with respect to a relation F≼G defined on L to mean that G is a provable consequence of F and the set of axioms T. Let us denote by HT the Heyting algebra so obtained. Then HT satisfies the same universal property as H0 above, but with respect to Heyting algebras H and families of elements 〈ai〉 satisfying the property that J(〈ai〉)=1 for any axiom J(〈Ai〉) in T. (Let us note that HT, taken with the family of its elements 〈[Ai]〉, itself satisfies this property.) The existence and uniqueness of the morphism is proved the same way as for H0, except that one must modify the implication 1→2 in "Provable identities" so that 1 reads "provably true from T," and 2 reads "any elements a1, a2,..., an in H satisfying the formulas of T."The Heyting algebra HT that we have just defined can be viewed as a quotient of the free Heyting algebra H0 on the same set of variables, by applying the universal property of H0 with respect to HT, and the family of its elements 〈[Ai]〉.
Every Heyting algebra is isomorphic to one of the form HT. To see this, let H be any Heyting algebra, and let 〈ai: i∈I〉 be a family of elements generating H (for example, any surjective family). Now consider the set T of formulas J(〈Ai〉) in the variables 〈Ai: i∈I〉 such that J(〈ai〉)=1. Then we obtain a morphism f:HT→H by the universal property of HT, which is clearly surjective. It is not difficult to show that f is injective.
Comparison to Lindenbaum algebras
The constructions we have just given play an entirely analogous role with respect to Heyting algebras to that of Lindenbaum algebras with respect to Boolean algebras. In fact, The Lindenbaum algebra BT in the variables {Ai} with respect to the axioms T is just our HT∪T1, where T1 is the set of all formulas of the form ¬¬F→F, since the additional axioms of T1 are the only ones that need to be added in order to make all classical tautologies provable.Heyting algebras as applied to intuitionistic logic
If one interprets the axioms of the intuitionistic propositional logic as terms of a Heyting algebra, then they will evaluate to the largest element, 1, in any Heyting algebra under any assignment of values to the formula's variables. For instance, is, by definition of the pseudo-complement, the largest element x such that . This inequation is satisfied for any x, so the largest such x is 1.Furthermore the rule of modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
allows us to derive the formula Q from the formulas P and P → Q. But in any Heyting algebra, if P has the value 1, and P → Q has the value 1, then it means that
, and so ; it can only be that Q has the value 1.This means that if a formula is deducible from the laws of intuitionistic logic, being derived from its axioms by way of the rule of modus ponens, then it will always have the value 1 in all Heyting algebras under any assignment of values to the formula's variables. However one can construct a Heyting algebra in which the value of Peirce's law is not always 1. Consider the 3-element algebra {0,½,1} as given above. If we assign ½ to P and 0 to Q, then the value of Peirce's law ((P → Q) → P) → P is ½. It follows that Peirce's law cannot be intuitionistically derived. See Curry–Howard isomorphism for the general context of what this implies in type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
.
The converse can be proven as well: if a formula always has the value 1, then it is deducible from the laws of intuitionistic logic, so the intuitionistically valid formulas are exactly those that always have a value of 1. This is similar to the notion that classically valid formulas are those formulas that have a value of 1 in the two-element Boolean algebra under any possible assignment of true and false to the formula's variables — that is, they are formulas which are tautologies in the usual truth-table sense. A Heyting algebra, from the logical standpoint, is then a generalization of the usual system of truth values, and its largest element 1 is analogous to 'true'. The usual two-valued logic system is a special case of a Heyting algebra, and the smallest non-trivial one, in which the only elements of the algebra are 1 (true) and 0 (false).
Decision problems
The problem of whether a given equation holds in every Heyting algebra was shown to be decidable by S. Kripke in 1965. The precise computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of the problem was established by R. Statman in 1979, who showed it was PSPACE-complete and hence at least as hard as deciding equations of Boolean algebra (shown NP-complete in 1971 by S. Cook) and conjectured to be considerably harder. The elementary or first-order theory of Heyting algebras is undecidable. It remains open whether the universal Horn theory of Heyting algebras, or word problem
Word problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
, is decidable. Apropos of the word problem it is known that Heyting algebras are not locally finite (no Heyting algebra generated by a finite nonempty set is finite), in contrast to Boolean algebras which are locally finite and whose word problem is decidable. It is unknown whether free complete Heyting algebras exist except in the case of a single generator where the free Heyting algebra on one generator is trivially completable by adjoining a new top.
See also
- Superintuitionistic (aka intermediate) logicIntermediate logicIn mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
s - List of Boolean algebra topics