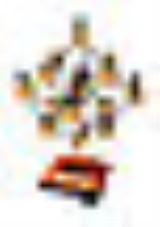
Logic alphabet
Encyclopedia
The logic alphabet constitutes an iconic set of symbol
s that systematically represents the sixteen possible binary truth functions of logic
. The logic alphabet was developed by Dr. Shea Zellweger
. Dr. Zellweger, now retired, was Chair of the Psychology Department for Mount Union College
and served as a Professor of Experimental Psychology
for over twenty five years. He has numerous published articles and has been a keynote speaker on human notation and sign system engineering at various semiotic symposia. The major emphasis of his iconic "logic alphabet" is to provide a more cognitively ergonomic notation for logic. Dr. Zellweger's visually iconic system more readily reveals, to the novice and expert alike, the underlying symmetry
relationships and geometric properties of the sixteen binary connectives within Boolean algebra.
s of truth values to truth values. A unary
truth function, for example, takes a single truth value and maps it onto another truth value. Similarly, a binary
truth function maps ordered pair
s of truth values onto truth values, while a ternary
truth function maps ordered triples of truth values onto truth values, and so on.
In the unary case, there are two possible inputs, viz. T and F, and thus four possible unary truth functions: one mapping T to T and F to F, one mapping T to F and F to F, one mapping T to T and F to T, and finally one mapping T to F and F to T, this last one corresponding to the familiar operation of logical negation. In the form of a table, the four unary truth functions may be represented as follows.
In the binary case, there are four possible inputs, viz. (T,T), (T,F), (F,T), and (F,F), thus yielding sixteen possible binary truth functions. Quite generally, for any number n, there are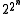
possible n-ary
truth functions. The sixteen possible binary truth functions are listed in the table below.
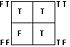
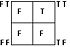
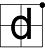
logic alphabet offers a visually systematic way of representing each of the sixteen binary truth functions. The idea behind the logic alphabet is to first represent the sixteen binary truth functions in the form of a square matrix rather than the more familiar tabular format seen in the table above, and then to assign a letter
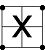
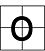
shape to each of these matrices. Letter shapes are derived from the distribution of Ts in the matrix. When drawing a logic symbol, one passes through each square with assigned F values while stopping in a square with assigned T values. In the extreme examples, the symbol for tautology
is a X (stops in all four squares), while the symbol for contradiction
is an O (passing through all squares without stopping). The square matrix corresponding to each binary truth function, as well as its corresponding letter shape, are displayed in the table below.
(viz. 'h') across the vertical axis we produce the symbol for ←, whereas by reflecting it across the horizontal axis we produce the symbol for →
, and by reflecting it across both the horizontal and vertical axes we produce the symbol for ∨
. Similar geometrical transformation can be obtained by operating upon the other symbols. Indeed, Zellweger
has constructed intriguing structures involving the symbols of the logic alphabet on the basis of these symmetries (http://www.logic-alphabet.net/images/logicbug_2345_2.jpg http://www.logic-alphabet.net/images/clockcompass_2353_2.jpg). The considerable aesthetic appeal of the logic alphabet has led to exhibitions of Zellweger's
work at the Museum of Jurassic Technology
in Los Angeles
, among other places.
The value of the logic alphabet lies in its use as a visually simpler pedagogical tool than the traditional system for logic notation. The logic alphabet eases the introduction to the fundamentals of logic, especially for children, at much earlier stages of cognitive development. Because the logic notation system, in current use today, is so deeply embedded in our computer culture, the "logic alphabets" adoption and value by the field of logic
itself, at this juncture, is questionable. Additionally, systems of natural deduction
, for example, generally require introduction and elimination rules for each connective, meaning that the use of all sixteen binary connectives would result in a highly complex proof
system. Various subsets of the sixteen binary connectives (e.g. {∨,&,→,~}, {∨,~}, {&, ~}, {→,~}) are themselves functionally complete in that they suffice to define the remaining connectives. In fact, both NAND
and NOR
are sole sufficient operators, meaning that the remaining connectives can all be defined solely in terms of either of them.
Symbol (formal)
For other uses see Symbol In logic, symbols build literal utility to illustrate ideas. A symbol is an abstraction, tokens of which may be marks or a configuration of marks which form a particular pattern...
s that systematically represents the sixteen possible binary truth functions of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
. The logic alphabet was developed by Dr. Shea Zellweger
Shea Zellweger
Shea Zellweger served as Chair of the Psychology Department at the University of Mount Union from 1969 to 1992. Professor Zellweger’s lifetime achievements and academic contributions to education continue to be significant. He received his Ph.D. in Experimental Psychology at Temple University in...
. Dr. Zellweger, now retired, was Chair of the Psychology Department for Mount Union College
Mount Union College
The University of Mount Union is a 4-year private, coeducational, liberal arts college in Alliance, Ohio.Mount Union enrolls 2200 undergraduates. Approximately 50 percent are women and 50 percent are men, representing more than 22 states and 13 countries. Mount Union has an active alumni base of...
and served as a Professor of Experimental Psychology
Experimental psychology
Experimental psychology is a methodological approach, rather than a subject, and encompasses varied fields within psychology. Experimental psychologists have traditionally conducted research, published articles, and taught classes on neuroscience, developmental psychology, sensation, perception,...
for over twenty five years. He has numerous published articles and has been a keynote speaker on human notation and sign system engineering at various semiotic symposia. The major emphasis of his iconic "logic alphabet" is to provide a more cognitively ergonomic notation for logic. Dr. Zellweger's visually iconic system more readily reveals, to the novice and expert alike, the underlying symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
relationships and geometric properties of the sixteen binary connectives within Boolean algebra.
Truth functions
Truth functions are functions from sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of truth values to truth values. A unary
Unary
* Unary numeral system, the simplest numeral system to represent natural numbers* Unary operation, a kind of mathematical operator that has only one operand* Unary coding, an entropy encoding that represents a number n with n − 1 ones followed by a zero...
truth function, for example, takes a single truth value and maps it onto another truth value. Similarly, a binary
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
truth function maps ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of truth values onto truth values, while a ternary
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
truth function maps ordered triples of truth values onto truth values, and so on.
In the unary case, there are two possible inputs, viz. T and F, and thus four possible unary truth functions: one mapping T to T and F to F, one mapping T to F and F to F, one mapping T to T and F to T, and finally one mapping T to F and F to T, this last one corresponding to the familiar operation of logical negation. In the form of a table, the four unary truth functions may be represented as follows.
| p | p | F | T | ~p |
|---|---|---|---|---|
| T | T | F | T | F |
| F | F | F | T | T |
In the binary case, there are four possible inputs, viz. (T,T), (T,F), (F,T), and (F,F), thus yielding sixteen possible binary truth functions. Quite generally, for any number n, there are
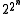possible n-aryArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
truth functions. The sixteen possible binary truth functions are listed in the table below.
| p | q | T | NAND | → | ~p | ← | ~q | ↔ | NOR | ∨ | XOR | q | N← | p | N→ | & | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | T | F | T | F | T | F | T | F | T | F | T | F | T | F | T | F |
| T | F | T | T | F | F | T | T | F | F | T | T | F | F | T | T | F | F |
| F | T | T | T | T | T | F | F | F | F | T | T | T | T | F | F | F | F |
| F | F | T | T | T | T | T | T | T | T | F | F | F | F | F | F | F | F |
The logic alphabet
Dr. Zellweger'sZellweger
The name Zellweger is a noble lineage of the Appenzell and may refer to:People with the surname Zellweger:* Marc Zellweger , Swiss football defender* Renée Zellweger , Academy Award-winning American film actress...
logic alphabet offers a visually systematic way of representing each of the sixteen binary truth functions. The idea behind the logic alphabet is to first represent the sixteen binary truth functions in the form of a square matrix rather than the more familiar tabular format seen in the table above, and then to assign a letter
Letter (alphabet)
A letter is a grapheme in an alphabetic system of writing, such as the Greek alphabet and its descendants. Letters compose phonemes and each phoneme represents a phone in the spoken form of the language....
shape to each of these matrices. Letter shapes are derived from the distribution of Ts in the matrix. When drawing a logic symbol, one passes through each square with assigned F values while stopping in a square with assigned T values. In the extreme examples, the symbol for tautology
Tautology
Tautology may refer to:*Tautology , using different words to say the same thing even if the repetition does not provide clarity. Tautology also means a series of self-reinforcing statements that cannot be disproved because the statements depend on the assumption that they are already...
is a X (stops in all four squares), while the symbol for contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
is an O (passing through all squares without stopping). The square matrix corresponding to each binary truth function, as well as its corresponding letter shape, are displayed in the table below.
| Conventional symbol | Matrix | Logic alphabet shape |
|---|---|---|
| T |  |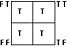
 |
| NAND Nand NAND may stand for:*Nand , an Indian classical raga.*Logical NAND , a binary operation in logic.**NAND gate, an electronic gate that implements a logical NAND.... |
 |
 |
| → Material conditional The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional... |
 |
 |
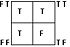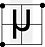| ~p |  |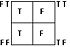
 |
| ← |  |
 |
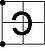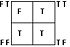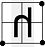| ~q |  |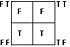
 |
| ↔ |  |
 |
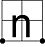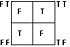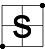| Logical NOR Logical NOR In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false... |
 |
 |
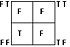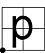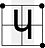
| ∨ Logical disjunction In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are... |
 |
 |
| XOR |  |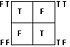
 |
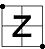| q |  |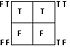
 |
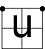| N← |  |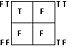
 |
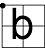| p |  |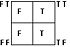
 |
| N→ |  |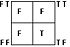
 |
| ∧ Logical conjunction In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false.... |
 |
 |
| F |  |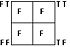
 |
Significance
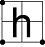
The interest of the logic alphabet lies in its aesthetic, symmetric, and geometric qualities that allow an individual to more easily, rapidly and visually manipulate the relationships between entire truth tables. For example, by reflecting the symbol for NANDNand
NAND may stand for:*Nand , an Indian classical raga.*Logical NAND , a binary operation in logic.**NAND gate, an electronic gate that implements a logical NAND....
(viz. 'h') across the vertical axis we produce the symbol for ←, whereas by reflecting it across the horizontal axis we produce the symbol for →
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
, and by reflecting it across both the horizontal and vertical axes we produce the symbol for ∨
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
. Similar geometrical transformation can be obtained by operating upon the other symbols. Indeed, Zellweger
Shea Zellweger
Shea Zellweger served as Chair of the Psychology Department at the University of Mount Union from 1969 to 1992. Professor Zellweger’s lifetime achievements and academic contributions to education continue to be significant. He received his Ph.D. in Experimental Psychology at Temple University in...
has constructed intriguing structures involving the symbols of the logic alphabet on the basis of these symmetries (http://www.logic-alphabet.net/images/logicbug_2345_2.jpg http://www.logic-alphabet.net/images/clockcompass_2353_2.jpg). The considerable aesthetic appeal of the logic alphabet has led to exhibitions of Zellweger's
Shea Zellweger
Shea Zellweger served as Chair of the Psychology Department at the University of Mount Union from 1969 to 1992. Professor Zellweger’s lifetime achievements and academic contributions to education continue to be significant. He received his Ph.D. in Experimental Psychology at Temple University in...
work at the Museum of Jurassic Technology
Museum of Jurassic Technology
The Museum of Jurassic Technology is an educational institution dedicated to the advancement of knowledge and the public appreciation of the lower jurassic...
in Los Angeles
Los Ángeles
Los Ángeles is the capital of the province of Biobío, in the commune of the same name, in Region VIII , in the center-south of Chile. It is located between the Laja and Biobío rivers. The population is 123,445 inhabitants...
, among other places.
The value of the logic alphabet lies in its use as a visually simpler pedagogical tool than the traditional system for logic notation. The logic alphabet eases the introduction to the fundamentals of logic, especially for children, at much earlier stages of cognitive development. Because the logic notation system, in current use today, is so deeply embedded in our computer culture, the "logic alphabets" adoption and value by the field of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
itself, at this juncture, is questionable. Additionally, systems of natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
, for example, generally require introduction and elimination rules for each connective, meaning that the use of all sixteen binary connectives would result in a highly complex proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
system. Various subsets of the sixteen binary connectives (e.g. {∨,&,→,~}, {∨,~}, {&, ~}, {→,~}) are themselves functionally complete in that they suffice to define the remaining connectives. In fact, both NAND
Nand
NAND may stand for:*Nand , an Indian classical raga.*Logical NAND , a binary operation in logic.**NAND gate, an electronic gate that implements a logical NAND....
and NOR
Nor
Nor may refer to:*In grammar, nor is a coordinating conjunction*Nór, the eponymous founder-king of Norway in Norse mythology*Nor , a character in the book in Wicked...
are sole sufficient operators, meaning that the remaining connectives can all be defined solely in terms of either of them.
See also
- Polish notationPolish notationPolish notation, also known as prefix notation, is a form of notation for logic, arithmetic, and algebra. Its distinguishing feature is that it places operators to the left of their operands. If the arity of the operators is fixed, the result is a syntax lacking parentheses or other brackets that...
- Propositional logic
- Boolean function
- Boolean algebra (logic)
- Logic gateLogic gateA logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
External links
- Page dedicated to Zellweger's logic alphabet
- Exhibition in a small museumMuseum of Jurassic TechnologyThe Museum of Jurassic Technology is an educational institution dedicated to the advancement of knowledge and the public appreciation of the lower jurassic...
: Flickr photopage, including a discussion between Tilman Piesk and probably Shea ZellwegerShea ZellwegerShea Zellweger served as Chair of the Psychology Department at the University of Mount Union from 1969 to 1992. Professor Zellweger’s lifetime achievements and academic contributions to education continue to be significant. He received his Ph.D. in Experimental Psychology at Temple University in...