Shea Zellweger
Encyclopedia
Shea Zellweger served as Chair of the Psychology Department at the University of Mount Union from 1969 to 1992. Professor Zellweger’s lifetime achievements and academic contributions to education continue to be significant. He received his Ph.D. in Experimental Psychology
at Temple University
in 1966. His doctoral dissertation focused on early visual stimulation experience and its later effects on discrimination learning. Zellweger is probably best known for his creation of a simpler and more mentally intuitive system of logic notation
called the logic alphabet
or X-stem Logic Alphabet (XLA). The XLA notation system contains a unique and visually iconographic approach to learning and performing logic operations. Patents have been issued on its design in the United States, Canada and Japan. (Link to USPTO Patent #: 4,273,542)
Zellweger’s background is a combination of formal education and extensive research in the fields of Psychology
, Pedagogy
, Semiotics
and Logic
. In 1949, Zellweger attended a summer seminar at the Institute of General Semantics
with Alfred Korzybski
. In 1949–52, still in the era of Robert M. Hutchins and the Great Books Program, he earned his undergraduate degree at the University of Chicago. In 1975–76, he spent a year at the Biological Computer Laboratory
, University of Illinois at Urbana-Champaign
, under the direction of Heinz von Foerster
. In 1982, while on sabbatical leave at the Peirce Edition Project, in Indianapolis (IUPUI), he examined and carefully reordered a 900 page section of manuscripts written by Charles Sanders Peirce entitled “The Simplest Mathematics” (1902). In 1989, he served the Peirce Edition Project again when he added to the proper sequencing of specific sections of Peirce’s extensive manuscripts. These multidisciplinary experiences contributed to the development, over a forty year period, of his X-stem Logic Alphabet. Zellweger has been a respected academic speaker and author, especially in the fields of Semiotics
and Education
.
Zellweger’s publications, as well as his unpublished materials, are extensive. A general principle expressed throughout his writings is the need for conscious and deliberate efforts that focus on the sign design and sign engineering of any and all kinds of notation (e.g. natural language
and its specialized systems of logical, mathematical, chemical and musical notation). Moreover, his publications primarily center on the formal language
of logic
and improving the structure of its symbols. Specifically, he focuses on the deliberate engineering of a constructed language
for logic called the X-stem Logic Alphabet (XLA). He emphasizes, with the mounting global prevalence of computers or “logic machines”, the importance of adopting a higher standard for the way we write and communicate logic. He brings to light the importance of a carefully constructed user-friendly notation that would allow students, at earlier stages of cognitive development
, to learn and incorporate the fundamental skills of logic. He further highlights the importance of purposely designing our symbols of notation to be as cognitively ergonomic as possible, while simultaneously possessing multiple layers of rich content. The fundamental and applied principles of semiotic engineering are exemplified throughout his publications.
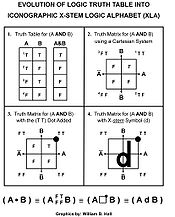
’s dot-X notation (1942). It could be said that XLA (1961–62) is the evolutionary product of the comprehensive work of Peirce, McCulloch, and Zellweger, or PMZ as an acronym. The standard notation used today (dot Logical conjunction
, vee Logical disjunction
, horseshoe Material conditional
representing and, or, if) is a lingering, overly abstract, unsystematically selected set of symbols that was primarily developed and used by Peano, Whitehead, and Russell, or by common acronym PWR. This already exposes the primary weakness. Dot, vee, horseshoe do not carry any information that identifies, specifies, and encodes the truth tables they represent, namely, TFFF, TTTF, and TFTT. In marked contrast, XLA is an intentionally engineered set of sixteen iconographic letter shape symbols specifically designed to improve the efficiency of learning and performing logical operations. Serving as a system of highly abbreviated mini truth tables, Zellweger’s claim is that XLA is not only much easier to learn. It is also much easier to use. In fact, when ten-base numerals are used without the abacus and when XLA is used without written laid out rows and columns of truth tables, ordinary operations in both notations are easier to perform during the act of computational writing.
It can be said that the current PWR symbols are to logic what Roman Numerals
are to arithmetic. Roman Numerals (I, II, III) were cumbersome to use and only maintained a dominant role in arithmetic until 1202, when Leonardo Fibonacci in his work Liber Abaci
, demonstrated that calculations with Hindu-Arabic numerals
(1, 2, 3) were far more efficient. The lack of mental and written efficiency in the use of traditional PWR symbols may be because they are not icons. Therefore, these extremely abstract symbols cannot in writing visually depict the truth tables themselves, the simple geometric forms, the notational symmetry
relations, and the isomorphic sets of interrelations inherent in logic. Conversely, the XLA symbols are iconographic and they possess a shape value. This enables complex logical operations to be performed through easy flips and rotations of the letter shape symbols themselves.
By design, the letter shape of each X-stem Logic Alphabet symbol visually embodies and displays its individual underlying logic truth table
. In other words, after the simple and exact truth table code in the deep structure of XLA has been learned, operations performed on the letter shape symbols are equivalent to logical operations acting on highly abbreviated sets of mini truth tables. Consequently, those using XLA never have the need to interrupt their calculations to check rows and columns of laid out truth tables. This basic and central advantage of XLA over PWR is often not fully recognized, even by practiced logicians. Nonetheless, systems of notation evolve and improve over time (e.g. Roman Numerals to the Decimal System and Imperial Units to the Metric System).
In brief, XLA is described in two steps: (1) give the 16 binary connectives the right geometry, the right shape value anatomy; and (2) add the transformational physiology, namely, apply the algebra of simple symmetry groups to the 16 iconic letter shape symbols. Change comes with a whisper. This whisper presents a triple isomorphism. The mental operations are the same as the symmetry operations are the same as the logical operations. Said the other way around, the logical operations are the same as the symmetry operations are the same as the mental operations. Said again in a different order, the logical operations are the same as the mental operations are the same as the symmetry operations. Here we have a prime example of cognitive ergonomics at its best. The single act of performing any one automatically performs the other two.
Whether or not the (PMZ) (XLA) system, or something similar to it, replaces the traditional PWR symbols remains to be seen. Nonetheless, for researchers and semioticians, Zellweger's contributions to logic notation will most likely play a valuable role in future developments.
Zellweger’s teaching system, for logic, integrates the developmental and interactive approaches of Fröbel, Montessori, and Piaget
. This is accomplished through the use of educational tools and models that predominantly focus on visual and kinesthetic learning modalities. At every level in the educational ladder, students of Zellweger’s system learn in a natural and intuitive way through the use of sensory-motor exercises and a variety of interactive geometric models. These models, at the most advanced level, become extremely complex and beautiful.
Each X-stem Logic Alphabet symbol can be easily flipped or rotated, by eye-hand coordination, through a series of simple symmetry transformations. When a student can visually and manually observe the geometry
and the network of symmetry
relationships among all 16 binary connectives of two-valued logic, it then becomes far easier for them to perform what are normally considered to be highly abstract logical operations. Zellweger’s publications and models permit students to literally “see”, “touch”, “play with”, “work with”, and “think about” the natural beauty of logic. His work is now on display at the Museum of Jurassic Technology, Culver City, California. (See Flickr image: http://www.flickr.com/photos/43992178@N00/387339135/)
Experimental psychology
Experimental psychology is a methodological approach, rather than a subject, and encompasses varied fields within psychology. Experimental psychologists have traditionally conducted research, published articles, and taught classes on neuroscience, developmental psychology, sensation, perception,...
at Temple University
Temple University
Temple University is a comprehensive public research university in Philadelphia, Pennsylvania, United States. Originally founded in 1884 by Dr. Russell Conwell, Temple University is among the nation's largest providers of professional education and prepares the largest body of professional...
in 1966. His doctoral dissertation focused on early visual stimulation experience and its later effects on discrimination learning. Zellweger is probably best known for his creation of a simpler and more mentally intuitive system of logic notation
Notation
-Written communication:* Phonographic writing systems, by definition, use symbols to represent components of auditory language, i.e. speech, which in turn refers to things or ideas. The two main kinds of phonographic notational system are the alphabet and syllabary...
called the logic alphabet
Logic alphabet
The logic alphabet constitutes an iconic set of symbols that systematically represents the sixteen possible binary truth functions of logic. The logic alphabet was developed by Dr. Shea Zellweger. Dr. Zellweger, now retired, was Chair of the Psychology Department for Mount Union College and served...
or X-stem Logic Alphabet (XLA). The XLA notation system contains a unique and visually iconographic approach to learning and performing logic operations. Patents have been issued on its design in the United States, Canada and Japan. (Link to USPTO Patent #: 4,273,542)
Background
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
, Pedagogy
Pedagogy
Pedagogy is the study of being a teacher or the process of teaching. The term generally refers to strategies of instruction, or a style of instruction....
, Semiotics
Semiotics
Semiotics, also called semiotic studies or semiology, is the study of signs and sign processes , indication, designation, likeness, analogy, metaphor, symbolism, signification, and communication...
and Logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
. In 1949, Zellweger attended a summer seminar at the Institute of General Semantics
Institute of General Semantics
The Institute of General Semantics is a not-for-profit corporation established in 1938 by Alfred Korzybski, to support research and publication on the topic of General Semantics. The Institute publishes Korzybski's writings, including the seminal text Science & Sanity, and books by other authors...
with Alfred Korzybski
Alfred Korzybski
Alfred Habdank Skarbek Korzybski was a Polish-American philosopher and scientist. He is remembered for developing the theory of general semantics...
. In 1949–52, still in the era of Robert M. Hutchins and the Great Books Program, he earned his undergraduate degree at the University of Chicago. In 1975–76, he spent a year at the Biological Computer Laboratory
Biological Computer Laboratory
The Biological Computer Laboratory was a research institute of the Department of Electrical Engineering at the University of Illinois at Urbana-Champaign. It was founded on 1 January 1958 by the then Professor of Electrical Engineering Heinz von Foerster...
, University of Illinois at Urbana-Champaign
University of Illinois at Urbana-Champaign
The University of Illinois at Urbana–Champaign is a large public research-intensive university in the state of Illinois, United States. It is the flagship campus of the University of Illinois system...
, under the direction of Heinz von Foerster
Heinz von Foerster
Heinz von Foerster was an Austrian American scientist combining physics and philosophy. Together with Warren McCulloch, Norbert Wiener, John von Neumann, Lawrence J. Fogel, and others, Heinz von Foerster was an architect of cybernetics.-Biography:Von Foerster was born in 1911 in Vienna, Austria,...
. In 1982, while on sabbatical leave at the Peirce Edition Project, in Indianapolis (IUPUI), he examined and carefully reordered a 900 page section of manuscripts written by Charles Sanders Peirce entitled “The Simplest Mathematics” (1902). In 1989, he served the Peirce Edition Project again when he added to the proper sequencing of specific sections of Peirce’s extensive manuscripts. These multidisciplinary experiences contributed to the development, over a forty year period, of his X-stem Logic Alphabet. Zellweger has been a respected academic speaker and author, especially in the fields of Semiotics
Semiotics
Semiotics, also called semiotic studies or semiology, is the study of signs and sign processes , indication, designation, likeness, analogy, metaphor, symbolism, signification, and communication...
and Education
Education
Education in its broadest, general sense is the means through which the aims and habits of a group of people lives on from one generation to the next. Generally, it occurs through any experience that has a formative effect on the way one thinks, feels, or acts...
.
Publications
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
and its specialized systems of logical, mathematical, chemical and musical notation). Moreover, his publications primarily center on the formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and improving the structure of its symbols. Specifically, he focuses on the deliberate engineering of a constructed language
Constructed language
A planned or constructed language—known colloquially as a conlang—is a language whose phonology, grammar, and/or vocabulary has been consciously devised by an individual or group, instead of having evolved naturally...
for logic called the X-stem Logic Alphabet (XLA). He emphasizes, with the mounting global prevalence of computers or “logic machines”, the importance of adopting a higher standard for the way we write and communicate logic. He brings to light the importance of a carefully constructed user-friendly notation that would allow students, at earlier stages of cognitive development
Cognitive development
Cognitive development is a field of study in neuroscience and psychology focusing on a child's development in terms of information processing, conceptual resources, perceptual skill, language learning, and other aspects of brain development and cognitive psychology compared to an adult's point of...
, to learn and incorporate the fundamental skills of logic. He further highlights the importance of purposely designing our symbols of notation to be as cognitively ergonomic as possible, while simultaneously possessing multiple layers of rich content. The fundamental and applied principles of semiotic engineering are exemplified throughout his publications.
Contribution
Zellweger’s contribution to the field of logic is best demonstrated through his development of the X-stem Logic Alphabet (XLA). The XLA notation is a highly advanced extension of both Charles Sanders Peirce’s box-X notation (1902) and Warren Sturgis McCullochWarren Sturgis McCulloch
Warren Sturgis McCulloch was an American neurophysiologist and cybernetician, known for his work on the foundation for certain brain theories and his contribution to the cybernetics movement.- Biography :...
’s dot-X notation (1942). It could be said that XLA (1961–62) is the evolutionary product of the comprehensive work of Peirce, McCulloch, and Zellweger, or PMZ as an acronym. The standard notation used today (dot Logical conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, vee Logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
, horseshoe Material conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
representing and, or, if) is a lingering, overly abstract, unsystematically selected set of symbols that was primarily developed and used by Peano, Whitehead, and Russell, or by common acronym PWR. This already exposes the primary weakness. Dot, vee, horseshoe do not carry any information that identifies, specifies, and encodes the truth tables they represent, namely, TFFF, TTTF, and TFTT. In marked contrast, XLA is an intentionally engineered set of sixteen iconographic letter shape symbols specifically designed to improve the efficiency of learning and performing logical operations. Serving as a system of highly abbreviated mini truth tables, Zellweger’s claim is that XLA is not only much easier to learn. It is also much easier to use. In fact, when ten-base numerals are used without the abacus and when XLA is used without written laid out rows and columns of truth tables, ordinary operations in both notations are easier to perform during the act of computational writing.
It can be said that the current PWR symbols are to logic what Roman Numerals
Roman numerals
The numeral system of ancient Rome, or Roman numerals, uses combinations of letters from the Latin alphabet to signify values. The numbers 1 to 10 can be expressed in Roman numerals as:...
are to arithmetic. Roman Numerals (I, II, III) were cumbersome to use and only maintained a dominant role in arithmetic until 1202, when Leonardo Fibonacci in his work Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
, demonstrated that calculations with Hindu-Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
(1, 2, 3) were far more efficient. The lack of mental and written efficiency in the use of traditional PWR symbols may be because they are not icons. Therefore, these extremely abstract symbols cannot in writing visually depict the truth tables themselves, the simple geometric forms, the notational symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
relations, and the isomorphic sets of interrelations inherent in logic. Conversely, the XLA symbols are iconographic and they possess a shape value. This enables complex logical operations to be performed through easy flips and rotations of the letter shape symbols themselves.
By design, the letter shape of each X-stem Logic Alphabet symbol visually embodies and displays its individual underlying logic truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
. In other words, after the simple and exact truth table code in the deep structure of XLA has been learned, operations performed on the letter shape symbols are equivalent to logical operations acting on highly abbreviated sets of mini truth tables. Consequently, those using XLA never have the need to interrupt their calculations to check rows and columns of laid out truth tables. This basic and central advantage of XLA over PWR is often not fully recognized, even by practiced logicians. Nonetheless, systems of notation evolve and improve over time (e.g. Roman Numerals to the Decimal System and Imperial Units to the Metric System).
In brief, XLA is described in two steps: (1) give the 16 binary connectives the right geometry, the right shape value anatomy; and (2) add the transformational physiology, namely, apply the algebra of simple symmetry groups to the 16 iconic letter shape symbols. Change comes with a whisper. This whisper presents a triple isomorphism. The mental operations are the same as the symmetry operations are the same as the logical operations. Said the other way around, the logical operations are the same as the symmetry operations are the same as the mental operations. Said again in a different order, the logical operations are the same as the mental operations are the same as the symmetry operations. Here we have a prime example of cognitive ergonomics at its best. The single act of performing any one automatically performs the other two.
Whether or not the (PMZ) (XLA) system, or something similar to it, replaces the traditional PWR symbols remains to be seen. Nonetheless, for researchers and semioticians, Zellweger's contributions to logic notation will most likely play a valuable role in future developments.
Teaching
Piaget
Piaget is surname of:* Edouard Piaget , Swiss entomologist* Jean Piaget , Swiss developmental psychologist* Paul Piaget , a Swiss rower...
. This is accomplished through the use of educational tools and models that predominantly focus on visual and kinesthetic learning modalities. At every level in the educational ladder, students of Zellweger’s system learn in a natural and intuitive way through the use of sensory-motor exercises and a variety of interactive geometric models. These models, at the most advanced level, become extremely complex and beautiful.
Each X-stem Logic Alphabet symbol can be easily flipped or rotated, by eye-hand coordination, through a series of simple symmetry transformations. When a student can visually and manually observe the geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and the network of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
relationships among all 16 binary connectives of two-valued logic, it then becomes far easier for them to perform what are normally considered to be highly abstract logical operations. Zellweger’s publications and models permit students to literally “see”, “touch”, “play with”, “work with”, and “think about” the natural beauty of logic. His work is now on display at the Museum of Jurassic Technology, Culver City, California. (See Flickr image: http://www.flickr.com/photos/43992178@N00/387339135/)