Monge cone
Encyclopedia
In the mathematical
theory of partial differential equation
s (PDE), the Monge cone is a geometrical object associated with a first-order equation. It is named for Gaspard Monge
. In two dimensions, let
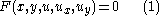
be a PDE for an unknown real-valued function u in two variables x and y. Assume that this PDE is non-degenerate in the sense that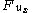
and 
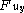are not both zero in the domain of definition. Fix a point (x0, y0, z0) and consider solution functions u which have
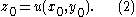
Each solution to (1) satisfying (2) determines the tangent plane to the graph
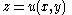
through the point (x0,y0,z0). As the pair (ux, uy) solving (1) varies, the tangent planes envelope
a cone in R3 with vertex at (x0,y0,z0), called the Monge cone. When F is quasilinear, the Monge cone degenerates to a single line called the Monge axis. Otherwise, the Monge cone is a proper cone since a nontrivial and non-coaxial one-parameter family of planes through a fixed point envelopes a cone. Explicitly, the original partial differential equation gives rise to a scalar-valued function on the cotangent bundle
of R3, defined at a point (x,y,z) by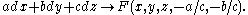
Vanishing of F determines a curve in the projective plane
with homogeneous coordinates
(a:b:c). The dual curve
is a curve in the projective tangent space
at the point, and the affine cone over this curve is the Monge cone. The cone may have multiple branches, each one an affine cone over a simple closed curve in the projective tangent space.
As the base point (x0,y0,z0) varies, the cone also varies. Thus the Monge cone is a cone field on R3. Finding solutions of (1) can thus be interpreted as finding a surface which is everywhere tangent to the Monge cone at the point. This is the method of characteristics
.
The technique generalizes to scalar first-order partial differential equations in n spatial variables; namely,
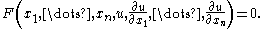
Through each point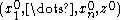
, the Monge cone (or axis in the quasilinear case) is the envelope of solutions of the PDE with 
.
The simplest fully nonlinear equation is the eikonal equation
. This has the form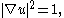
so that the function F is given by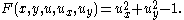
The dual cone consists of 1-forms adx+bdy+cdz satisfying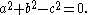
Taken projectively, this defines a circle. The dual curve is also a circle, and so the Monge cone at each point is a proper cone.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDE), the Monge cone is a geometrical object associated with a first-order equation. It is named for Gaspard Monge
Gaspard Monge
Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
. In two dimensions, let
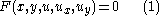
be a PDE for an unknown real-valued function u in two variables x and y. Assume that this PDE is non-degenerate in the sense that
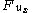and 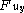are not both zero in the domain of definition. Fix a point (x0, y0, z0) and consider solution functions u which have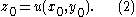Each solution to (1) satisfying (2) determines the tangent plane to the graph
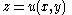
through the point (x0,y0,z0). As the pair (ux, uy) solving (1) varies, the tangent planes envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
a cone in R3 with vertex at (x0,y0,z0), called the Monge cone. When F is quasilinear, the Monge cone degenerates to a single line called the Monge axis. Otherwise, the Monge cone is a proper cone since a nontrivial and non-coaxial one-parameter family of planes through a fixed point envelopes a cone. Explicitly, the original partial differential equation gives rise to a scalar-valued function on the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of R3, defined at a point (x,y,z) by
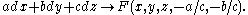
Vanishing of F determines a curve in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
with homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(a:b:c). The dual curve
Dual curve
In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree...
is a curve in the projective tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at the point, and the affine cone over this curve is the Monge cone. The cone may have multiple branches, each one an affine cone over a simple closed curve in the projective tangent space.
As the base point (x0,y0,z0) varies, the cone also varies. Thus the Monge cone is a cone field on R3. Finding solutions of (1) can thus be interpreted as finding a surface which is everywhere tangent to the Monge cone at the point. This is the method of characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
.
The technique generalizes to scalar first-order partial differential equations in n spatial variables; namely,
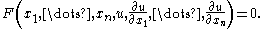
Through each point
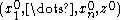, the Monge cone (or axis in the quasilinear case) is the envelope of solutions of the PDE with .Examples
Eikonal equationThe simplest fully nonlinear equation is the eikonal equation
Eikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
. This has the form
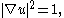
so that the function F is given by
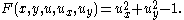
The dual cone consists of 1-forms adx+bdy+cdz satisfying
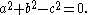
Taken projectively, this defines a circle. The dual curve is also a circle, and so the Monge cone at each point is a proper cone.