Monochromatic electromagnetic plane wave
Encyclopedia
In general relativity
, the monochromatic electromagnetic plane wave spacetime is the analog of the monochromatic plane waves known from Maxwell's theory. The precise definition of the solution is a bit complicated, but very instructive.
Any exact solution
of the Einstein field equation which models an electromagnetic field
must take into account all gravitational effects of the energy
of the electromagnetic field
itself. If there is no matter and no non-gravitational fields present other than the electromagnetic field, this means that we must simultaneously solve the Einstein field equation and the (curved spacetime, source-free) Maxwell field equations
.
In Maxwell's theory of electromagnetism
, one of the most important types of an electromagnetic field are those representing electromagnetic radiation
. Of these, the most important examples are the
electromagnetic plane waves, in which the radiation has planar wavefronts moving in a specific direction at the speed of light. Of these, the most basic are the monochromatic plane waves, in which only one frequency
component is present. This is precisely the phenomenon which our solution will model in terms of general relativity.
and frequency 
can be written, in terms of Rosen coordinates, in the form
where
is the first positive root of 
where 
. In this chart, 
are null
coordinate vectors while
are spacelike coordinate vectors.
Here, the Mathieu cosine
is an even function which solves the Mathieu equation and also takes the value 
. Despite the name, this function is not periodic, and it cannot be written in terms of sinusoidal or even hypergeometric functions. (See Mathieu function
for more about the Mathieu cosine function.)
In our expression for the metric, note that
are null vector
fields. Therefore
is a timelike vector field, while 
are spacelike vector fields.
To define the electromagnetic field, we may take the electromagnetic four-vector potential
We now have the complete specification of a mathematical model formulated in general relativity.
of Killing vector field
s. A convenient basis consists of one null vector field,
three spacelike vector fields,
and two additional vector fields,
Here,
generate the Euclidean group
, acting within each planar wavefront, which justifies the name plane wave for this solution. Also
show that all nontranverse directions are equivalent. This corresponds to the well-known fact that in flat spacetime, two colliding plane waves always collide head-on when represented in the appropriate Lorentz frame
.
For future reference we note that this six dimensional group of self-isometries acts transitively, so that our spacetime is homogeneous. However, it is not isotropic, since the transverse directions are distinguished from the non-transverse ones.
represents the local Lorentz frame defined by a family of nonspinning inertial observers. That is,
which means that the integral curve
s of the timelike unit vector field
are timelike geodesics, and also
which means that the spacelike unit vector fields
are nonspinning. (They are Fermi-Walker transported.) Here, 
is a timelike unit vector field, while 
are spacelike unit vector fields.
Nonspinning inertial frames are as close as we can come in curved spacetimes to the usual Lorentz frames known from special relativity
, where Lorentz transformations are simply changes from one Lorentz frame to another.
This electromagnetic field is a source-free solution of the Maxwell field equations on the particular curved spacetime which is defined by the metric tensor above. It is a null solution, and it represents a transverse sinusoidal electromagnetic plane wave with amplitude
and frequency 
, traveling in the 
direction. When we
we find that the Einstein field equation
is satisfied. This is what we mean by saying that we have an exact electrovacuum solution
.
In terms of our frame, the stress-energy tensor turns out to be
Notice that this is exactly the same expression that we would find in classical electromagnetism (where we neglect the gravitational effects of the electromagnetic field energy) for the null field given above; the only difference is that now our frame is a anholonomic (orthonormal) basis on a curved spacetime, rather than a coordinate basis in flat spacetime. (See frame fields
.)
are all constant along each world line, given by an integral curve of the timelike unit vector field 
. Thus, in the Rosen chart, these observers might appear to be motionless. But in fact they are in relative motion with respect to one another. To see this, we should compute their expansion tensor with respect to the frame given above. This turns out to be
where
. The nonvanishing components are identical, and are
Physically, this means that a small spherical 'cloud' of our inertial observers hovers momentarily at
and then begin to collapse, eventually passing through one another at 
. If we imagine them as forming a three dimensional cloud of uniformly distributed test particles, this collapse occurs orthogonal to the direction of propagation of the wave. The cloud exhibits no relative motion in the direction of propagation, so this is a purely transverse motion.
For
(the shortwave approximation), we have approximately
For example, with
, we have
where the exact expressions plotted in red and the shortwave approximations in green.
The vorticity tensor of our congruence vanishes identically, so the world lines of our observers are hypersurface orthogonal. The three-dimensional Riemann tensor of the hyperslices is given, with respect to our frame, by
So the curvature splits neatly into wave (the sectional curvatures parallel to the direction of propagation) and background (the transverse sectional curvature).
of the Riemann curvature tensor, taken with respect to
, is simplicity itself. The electrogravitic tensor
, which directly represents the tidal accelerations, is
The magnetogravitic tensor
, which directly represents the spin-spin force on a gyroscope carried by one of our observers, is
(The topogravitic tensor
, which represents the spatial sectional curvatures, agrees with the electrogravitic tensor.)
Looking back at our graph of the metric tensor, we can see that the tidal tensor produces small sinusoidal relative accelerations with period
, which are purely transverse to the direction of propagation of the wave. The net gravitational effect over many periods is to produce an expansion and recollapse cycle of our family of inertial nonspining observers. This can be considered the effect of the background curvature produced by the wave.
This expansion and recollapse cycle is reminiscent of the expanding and recollapsing FRW cosmological models, and it occurs for a similar reason: the presence of nongravitational mass-energy. In the FRW models, this mass-energy is due to the mass of the dust particles; here, it is due to the field energy of the electromagnetic field. There, the expansion-recollapse cycle begins and ends with a strong scalar curvature singularity; here, we have a mere coordinate singularity (a circumstance which much confused Einstein and Rosen in 1937). In addition, here we have a small sinusoidal modulation of the expansion and recollapse.
has vanishing optical scalars
, but the null geodesic congruence generated by
has vanishing twist and shear scalars but nonvanishing expansion scalar
This shows that when looking through departing wavefronts at distant objects, our inertial nonspinning observers will see their apparent size change exactly the same way as the expansion of the timelike geodesic congruence itself.
is a mere coordinate singularity is to recall that our spacetime is homogeneous, so that all events are equivalent. To confirm this directly, and to study from a different perspective the relative motion of our inertial nonspinning observers, we can apply the coordinate transformation
where
This brings the solution into its representation in terms of Brinkmann coordinates
:
Since it can be shown that the new coordinates are geodesically complete,
the Brinkmann coordinates define a global coordinate chart.
In this chart, we can see that an infinite sequence of identical expansion-recollapse cycles occur!
and so forth. Naturally, if we compute the expansion tensor, electrogravitic tensor, and so forth, we obtain exactly the same answers as before, but expressed in the new coordinates.
The simplicity of the metric tensor compared to the complexity of the frame is striking. The point is that we can more easily visualize the caustics
formed by the relative motion of our observers in the new chart. The integral curves of the timelike unit geodesic vector field
give the world lines of our observers. In the Rosen chart, these appear as vertical coordinate lines, since that chart is comoving.
To understand how this situation appears in the Brinkmann chart, notice that when
is large, our timelike geodesic unit vector field becomes approximately
Suppressing the last term, we have
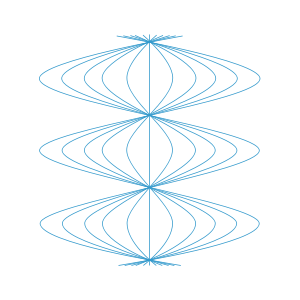
We immediately obtain an integral curve which exhibits sinusoidal expansion and reconvergence cycles. See the figure, in which time is running vertically and we use the radial symmetry to suppress one spatial dimension. This figure shows why there is a coordinate singularity in the Rosen chart; the observers must actually pass by one another at regular intervals, which is obviously incompatible with the comoving property, so the chart breaks down at these places. Note that this figure incorrectly suggests that one observer is the 'center of attraction', as it were, but in fact they are all completely equivalent, due to the large symmetry group of this spacetime. Note too that the broadly sinusoidal relative motion of our observers is fully consistent with the behavior of the expansion tensor (with respect to the frame field corresponding to our family of observers) which was noted above.
It is worth noting that these somewhat tricky points confused no less a figure than Albert Einstein
in his 1937 paper on gravitational waves (written long before the modern mathematical machinery used here was widely appreciated in physics).
Thus, in the Brinkmann chart, the world lines of our observers, in the shortwave case, are periodic curves which have the form of sinusoidals with period
, modulated by much smaller sinusoidal perturbations in the null direction 
and having a much shorter period, 
. The observers periodically expand and recollapse transversely to the direct of propagation; this motion is modulated by short period small amplitude perturbations.
(i.e., as a wave in flat spacetime, neglecting the gravitational effects of the energy of the electromagnetic field), we see that the striking new feature in general relativity is the expansion and collapse cycles experienced by our observers, which we can put down to background curvature, not any measurements made over short times and distances (on the order of the wavelength of the electromagnetic radiation).
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the monochromatic electromagnetic plane wave spacetime is the analog of the monochromatic plane waves known from Maxwell's theory. The precise definition of the solution is a bit complicated, but very instructive.
Any exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equation which models an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
must take into account all gravitational effects of the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
itself. If there is no matter and no non-gravitational fields present other than the electromagnetic field, this means that we must simultaneously solve the Einstein field equation and the (curved spacetime, source-free) Maxwell field equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
In Maxwell's theory of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, one of the most important types of an electromagnetic field are those representing electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
. Of these, the most important examples are the
electromagnetic plane waves, in which the radiation has planar wavefronts moving in a specific direction at the speed of light. Of these, the most basic are the monochromatic plane waves, in which only one frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
component is present. This is precisely the phenomenon which our solution will model in terms of general relativity.
Definition of the solution
The metric tensor of the unique exact solution modeling a linearly polarized electromagnetic plane wave with amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and frequency can be written, in terms of Rosen coordinates, in the formwhere
is the first positive root of where . In this chart, are nullNull vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
coordinate vectors while
are spacelike coordinate vectors.Here, the Mathieu cosine
is an even function which solves the Mathieu equation and also takes the value . Despite the name, this function is not periodic, and it cannot be written in terms of sinusoidal or even hypergeometric functions. (See Mathieu functionMathieu function
In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...
for more about the Mathieu cosine function.)
In our expression for the metric, note that
are null vectorNull vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
fields. Therefore
is a timelike vector field, while are spacelike vector fields.To define the electromagnetic field, we may take the electromagnetic four-vector potential
Electromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
We now have the complete specification of a mathematical model formulated in general relativity.
Local isometries
Our spacetime is modeled by a Lorentzian manifold which has some remarkable symmetries. Namely, our spacetime admits a six dimensional Lie group of self-isometries. This group is generated by a six dimensional Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of Killing vector field
Killing vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
s. A convenient basis consists of one null vector field,
three spacelike vector fields,
and two additional vector fields,
Here,
generate the Euclidean groupEuclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, acting within each planar wavefront, which justifies the name plane wave for this solution. Also
show that all nontranverse directions are equivalent. This corresponds to the well-known fact that in flat spacetime, two colliding plane waves always collide head-on when represented in the appropriate Lorentz frameLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
.
For future reference we note that this six dimensional group of self-isometries acts transitively, so that our spacetime is homogeneous. However, it is not isotropic, since the transverse directions are distinguished from the non-transverse ones.
A family of inertial observers
The frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
represents the local Lorentz frame defined by a family of nonspinning inertial observers. That is,
which means that the integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the timelike unit vector field
are timelike geodesics, and alsowhich means that the spacelike unit vector fields
are nonspinning. (They are Fermi-Walker transported.) Here, is a timelike unit vector field, while are spacelike unit vector fields.Nonspinning inertial frames are as close as we can come in curved spacetimes to the usual Lorentz frames known from special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, where Lorentz transformations are simply changes from one Lorentz frame to another.
The electromagnetic field
With respect to our frame, the electromagnetic field obtained from the potential given above isThis electromagnetic field is a source-free solution of the Maxwell field equations on the particular curved spacetime which is defined by the metric tensor above. It is a null solution, and it represents a transverse sinusoidal electromagnetic plane wave with amplitude
and frequency , traveling in the direction. When we
- compute the stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
for the given electromagnetic field, - compute the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
for the given metric tensor,
we find that the Einstein field equation
is satisfied. This is what we mean by saying that we have an exact electrovacuum solutionElectrovacuum solution
In general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
.
In terms of our frame, the stress-energy tensor turns out to be
Notice that this is exactly the same expression that we would find in classical electromagnetism (where we neglect the gravitational effects of the electromagnetic field energy) for the null field given above; the only difference is that now our frame is a anholonomic (orthonormal) basis on a curved spacetime, rather than a coordinate basis in flat spacetime. (See frame fields
Frame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
.)
Relative motion of the observers
The Rosen chart is said to be comoving with our family of inertial nonspinning observers, because the coordinates are all constant along each world line, given by an integral curve of the timelike unit vector field . Thus, in the Rosen chart, these observers might appear to be motionless. But in fact they are in relative motion with respect to one another. To see this, we should compute their expansion tensor with respect to the frame given above. This turns out to bewhere
. The nonvanishing components are identical, and are
- concave down on
- vanish at
.
Physically, this means that a small spherical 'cloud' of our inertial observers hovers momentarily at
and then begin to collapse, eventually passing through one another at . If we imagine them as forming a three dimensional cloud of uniformly distributed test particles, this collapse occurs orthogonal to the direction of propagation of the wave. The cloud exhibits no relative motion in the direction of propagation, so this is a purely transverse motion.For
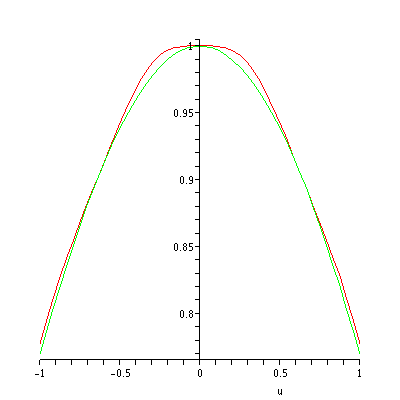
(the shortwave approximation), we have approximatelyFor example, with
, we have
 |
 |
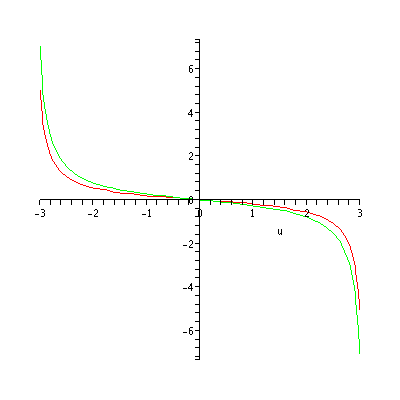where the exact expressions plotted in red and the shortwave approximations in green.
The vorticity tensor of our congruence vanishes identically, so the world lines of our observers are hypersurface orthogonal. The three-dimensional Riemann tensor of the hyperslices is given, with respect to our frame, by
So the curvature splits neatly into wave (the sectional curvatures parallel to the direction of propagation) and background (the transverse sectional curvature).
The Riemann curvature tensor
In contrast, the Bel decompositionBel decomposition
In semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann curvature tensor, taken with respect to
, is simplicity itself. The electrogravitic tensorElectrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
, which directly represents the tidal accelerations, is
The magnetogravitic tensor
Magnetogravitic tensor
In general relativity, the magnetogravitic tensor is one of the three pieces appearing in the Bel decomposition of the Riemann tensor.The magnetogravitic tensor can be interpreted physically as a specifying possible spin-spin forces on spinning bits of matter, such as spinning test particles....
, which directly represents the spin-spin force on a gyroscope carried by one of our observers, is
(The topogravitic tensor
Topogravitic tensor
In general relativity, the topogravitic tensor is one of the three pieces of the Bel decomposition of the Riemann tensor.The topogravitic tensor can be interpreted as representing the sectional curvatures for the spatial part of a frame field....
, which represents the spatial sectional curvatures, agrees with the electrogravitic tensor.)
Looking back at our graph of the metric tensor, we can see that the tidal tensor produces small sinusoidal relative accelerations with period
, which are purely transverse to the direction of propagation of the wave. The net gravitational effect over many periods is to produce an expansion and recollapse cycle of our family of inertial nonspining observers. This can be considered the effect of the background curvature produced by the wave.This expansion and recollapse cycle is reminiscent of the expanding and recollapsing FRW cosmological models, and it occurs for a similar reason: the presence of nongravitational mass-energy. In the FRW models, this mass-energy is due to the mass of the dust particles; here, it is due to the field energy of the electromagnetic field. There, the expansion-recollapse cycle begins and ends with a strong scalar curvature singularity; here, we have a mere coordinate singularity (a circumstance which much confused Einstein and Rosen in 1937). In addition, here we have a small sinusoidal modulation of the expansion and recollapse.
Optical effects
A general principle concerning plane waves states you cannot see the wave train enter the station, but you can see it leave. That is, if you look through oncoming wavefronts at distant objects, you will see no optical distortion, but if you turn and look through departing wavefronts at distanct object, you will see optical distortions. Specifically, the null geodesic congruence generated by the null vector field has vanishing optical scalarsOptical scalars
In general relativity, optical scalars are a set of scalars that describe various properties of null geodesic congruences. The three optical scalars used in general relativity are expansion, shear and twist and were first defined and used by Sachs...
, but the null geodesic congruence generated by
has vanishing twist and shear scalars but nonvanishing expansion scalarThis shows that when looking through departing wavefronts at distant objects, our inertial nonspinning observers will see their apparent size change exactly the same way as the expansion of the timelike geodesic congruence itself.
The Brinkmann chart
One way to quickly see the plausibility of the assertion that is a mere coordinate singularity is to recall that our spacetime is homogeneous, so that all events are equivalent. To confirm this directly, and to study from a different perspective the relative motion of our inertial nonspinning observers, we can apply the coordinate transformationwhere
This brings the solution into its representation in terms of Brinkmann coordinates
Brinkmann coordinates
Brinkmann coordinates are a particular coordinate system for a spacetime belonging to the family of pp-wave metrics. In terms of these coordinates, the metric tensor can be written asds^2 \, = H du^2 + 2 du dv + dx^2 + dy^2...
:
Since it can be shown that the new coordinates are geodesically complete,
the Brinkmann coordinates define a global coordinate chart.
In this chart, we can see that an infinite sequence of identical expansion-recollapse cycles occur!
Caustics
In the Brinkmann chart, our frame field becomes rather complicated:and so forth. Naturally, if we compute the expansion tensor, electrogravitic tensor, and so forth, we obtain exactly the same answers as before, but expressed in the new coordinates.
The simplicity of the metric tensor compared to the complexity of the frame is striking. The point is that we can more easily visualize the caustics
Caustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
formed by the relative motion of our observers in the new chart. The integral curves of the timelike unit geodesic vector field
give the world lines of our observers. In the Rosen chart, these appear as vertical coordinate lines, since that chart is comoving.To understand how this situation appears in the Brinkmann chart, notice that when
is large, our timelike geodesic unit vector field becomes approximatelySuppressing the last term, we have
We immediately obtain an integral curve which exhibits sinusoidal expansion and reconvergence cycles. See the figure, in which time is running vertically and we use the radial symmetry to suppress one spatial dimension. This figure shows why there is a coordinate singularity in the Rosen chart; the observers must actually pass by one another at regular intervals, which is obviously incompatible with the comoving property, so the chart breaks down at these places. Note that this figure incorrectly suggests that one observer is the 'center of attraction', as it were, but in fact they are all completely equivalent, due to the large symmetry group of this spacetime. Note too that the broadly sinusoidal relative motion of our observers is fully consistent with the behavior of the expansion tensor (with respect to the frame field corresponding to our family of observers) which was noted above.
It is worth noting that these somewhat tricky points confused no less a figure than Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in his 1937 paper on gravitational waves (written long before the modern mathematical machinery used here was widely appreciated in physics).
Thus, in the Brinkmann chart, the world lines of our observers, in the shortwave case, are periodic curves which have the form of sinusoidals with period
, modulated by much smaller sinusoidal perturbations in the null direction and having a much shorter period, . The observers periodically expand and recollapse transversely to the direct of propagation; this motion is modulated by short period small amplitude perturbations.Summary
Comparing our exact solution with the usual monochromatic electromagnetic plane wave as treated in special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
(i.e., as a wave in flat spacetime, neglecting the gravitational effects of the energy of the electromagnetic field), we see that the striking new feature in general relativity is the expansion and collapse cycles experienced by our observers, which we can put down to background curvature, not any measurements made over short times and distances (on the order of the wavelength of the electromagnetic radiation).
See also
- Sticky bead argumentSticky bead argumentIn general relativity, the sticky bead argument is a simple thought experiment designed to show that gravitational radiation is indeed predicted by general relativity, and can have physical effects...
, for an account of the 1937 paper by Einstein and Rosen alluded to above.