Mathieu function
Encyclopedia
In mathematics
, the Mathieu functions are certain special functions
useful for treating a variety of problems in applied mathematics, including
They were introduced by in the context of the first problem.
Closely related is Mathieu's modified differential equation
which follows on substitution
.
The substitution
transforms Mathieu's equation to the algebraic form
This has two regular singularities at
and one irregular singularity at infinity, which implies that in general (unlike many other special functions), the solutions of Mathieu's equation cannot be expressed in terms of hypergeometric functions.
Mathieu's differential equations arise as models in many contexts, including the stability of railroad rails as trains drive over them, seasonally forced population dynamics, the four-dimensional wave equation
, and the Floquet theory of the stability of limit cycles.
), for fixed values of a,q, Mathieu's equation admits a complex valued solution of form
where
is a complex number, the Mathieu exponent, and P is a complex valued function which is periodic in 
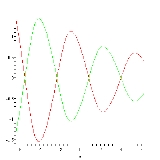
with period 
. However, P is in general not sinusoidal. In the example plotted below, 
(real part, red; imaginary part; green):
is a function of 
defined as the unique solution of the Mathieu equation which
Similarly, the Mathieu sine
is the unique solution which
These are real-valued functions which are closely related to the Floquet solution:
The general solution to the Mathieu equation (for fixed a,q) is a linear combination of the Mathieu cosine and Mathieu sine functions.
A noteworthy special case is
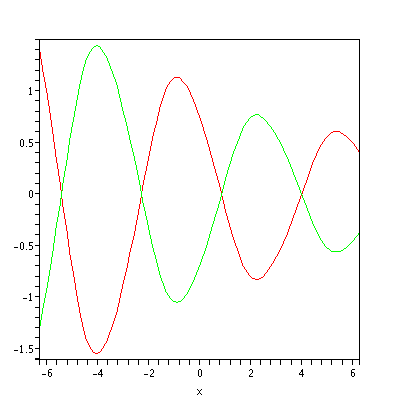
In general, the Mathieu sine and cosine are aperiodic. Nonetheless, for small values of q, we have approximately
For example:
, for countably many special values of 
, called characteristic values, the Mathieu equation admits solutions which are periodic with period 
. The characteristic values of the Mathieu cosine, sine functions respectively are written 
, where n is a natural number
. The periodic special cases of the Mathieu cosine and sine functions are often written
respectively, although they are traditionally given a different normalization (namely, that their L2 norm equal 
). Therefore, for positive q, we have
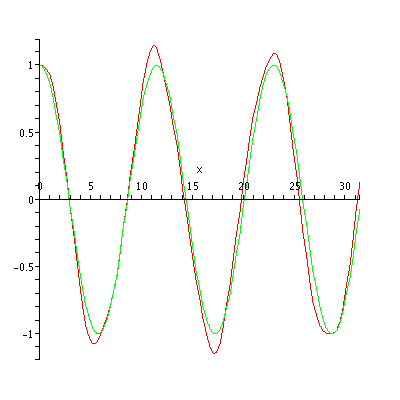
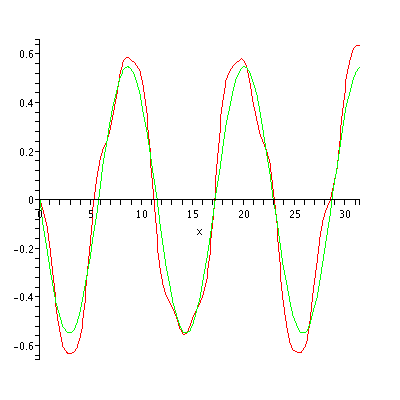
Here are the first few periodic Mathieu cosine functions for q = 1:
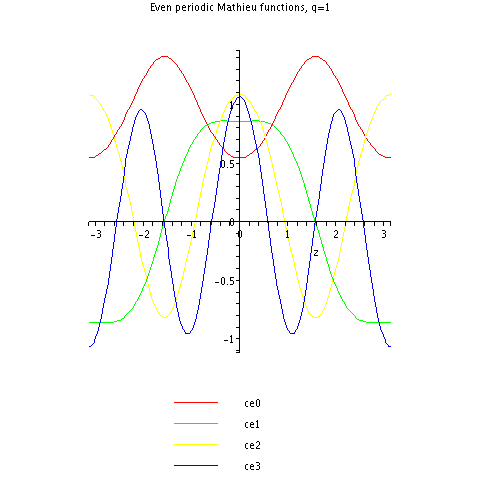
Note that, for example,
(green) resembles a cosine function, but with flatter hills and shallower valleys.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Mathieu functions are certain special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
useful for treating a variety of problems in applied mathematics, including
- vibrating elliptical drumheads,
- quadrupoleQuadrupoleA quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
s mass filters and quadrupole ion traps for mass spectrometryMass spectrometryMass spectrometry is an analytical technique that measures the mass-to-charge ratio of charged particles.It is used for determining masses of particles, for determining the elemental composition of a sample or molecule, and for elucidating the chemical structures of molecules, such as peptides and... - wave motion in periodic media, such as ultracold atoms in an optical latticeOptical latticeAn optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate in the locations of potential minima...
- the phenomenon of parametric resonance in forced oscillators,
- exact plane wave solutions in general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, - the Stark effectStark effectThe Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
for a rotating electric dipole, - in general, the solution of differential equations that are separableSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
in elliptic cylindrical coordinatesElliptic cylindrical coordinatesElliptic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional elliptic coordinate system in the...
.
They were introduced by in the context of the first problem.
Mathieu equation
The canonical form for Mathieu's differential equation isClosely related is Mathieu's modified differential equation
which follows on substitution
.The substitution
transforms Mathieu's equation to the algebraic formThis has two regular singularities at
and one irregular singularity at infinity, which implies that in general (unlike many other special functions), the solutions of Mathieu's equation cannot be expressed in terms of hypergeometric functions.Mathieu's differential equations arise as models in many contexts, including the stability of railroad rails as trains drive over them, seasonally forced population dynamics, the four-dimensional wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, and the Floquet theory of the stability of limit cycles.
Floquet solution
According to Floquet's theorem (or Bloch's theoremBloch's theorem
* For the theorem named after Felix Bloch on wave functions of a particle in a periodic potential, see Bloch wave.* For the theorem in complex variables named after André Bloch, see Bloch's theorem ....
), for fixed values of a,q, Mathieu's equation admits a complex valued solution of form
where
is a complex number, the Mathieu exponent, and P is a complex valued function which is periodic in with period . However, P is in general not sinusoidal. In the example plotted below, (real part, red; imaginary part; green):Mathieu sine and cosine
For fixed a,q, the Mathieu cosine is a function of defined as the unique solution of the Mathieu equation which
- takes the value
, - is an even function, hence
.
Similarly, the Mathieu sine
is the unique solution which
- takes the value
, - is an odd function, hence
.
These are real-valued functions which are closely related to the Floquet solution:
The general solution to the Mathieu equation (for fixed a,q) is a linear combination of the Mathieu cosine and Mathieu sine functions.
A noteworthy special case is
In general, the Mathieu sine and cosine are aperiodic. Nonetheless, for small values of q, we have approximately
For example:
Periodic solutions
Given, for countably many special values of , called characteristic values, the Mathieu equation admits solutions which are periodic with period . The characteristic values of the Mathieu cosine, sine functions respectively are written , where n is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. The periodic special cases of the Mathieu cosine and sine functions are often written
respectively, although they are traditionally given a different normalization (namely, that their L2 norm equal ). Therefore, for positive q, we haveHere are the first few periodic Mathieu cosine functions for q = 1:
Note that, for example,
(green) resembles a cosine function, but with flatter hills and shallower valleys.See also
- Monochromatic electromagnetic plane waveMonochromatic electromagnetic plane waveIn general relativity, the monochromatic electromagnetic plane wave spacetime is the analog of the monochromatic plane waves known from Maxwell's theory...
, an example of an important exact plane wave solution to the Einstein field equation in general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
which is expressed using Mathieu cosine functions. - Inverted pendulumInverted pendulumAn inverted pendulum is a pendulum which has its mass above its pivot point. It is often implemented with the pivot point mounted on a cart that can move horizontally and may be called a cart and pole...
- Lamé functionLamé functionIn mathematics, a Lamé function is a solution of Lamé's equation, a second-order ordinary differential equation. It was introduced in the paper . Lamé's equation appears in the method of separation of variables applied to the Laplace equation in elliptic coordinates...