Monotone class theorem
Encyclopedia
A monotone class in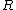 
is a collection 
of subsets of 
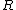which is closed
under countable monotone unions and intersections, i.e. if
and 
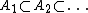then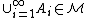 
, and similarly for intersections of decreasing sequences of sets.
The Monotone Class Theorem says that the smallest monotone class containing an algebra of sets
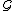is precisely the smallest σ-algebra
containing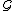
.
As a corollary, if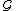
is a ring of sets, then the smallest monotone class containing it coincides with the sigma-ring of 
.
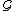This theorem is used as a type of transfinite induction
, and is used to prove many Theorems, such as Fubini's theorem
in basic measure theory.
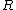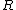is a collection of subsets of which is closedClosed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
under countable monotone unions and intersections, i.e. if
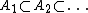and then 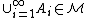, and similarly for intersections of decreasing sequences of sets.The Monotone Class Theorem says that the smallest monotone class containing an algebra of sets
Algebra of sets
The algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
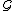is precisely the smallest σ-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
containing
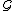.As a corollary, if
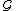is a ring of sets, then the smallest monotone class containing it coincides with the sigma-ring of 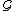.This theorem is used as a type of transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
, and is used to prove many Theorems, such as Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
in basic measure theory.