Ring of sets
Encyclopedia
In mathematics
, a nonempty collection of sets
is called a ring (of sets) if it is closed
under intersection
and symmetric difference
. That is, for any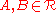
,
where
represents the symmetric difference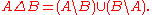
A ring of sets forms an algebraic ring
(possibly without unit) under these two operations. Intersection distributes over symmetric difference:
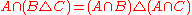
The empty set
is the identity element for
, and the union of all the sets, if it is in the ring, is the identity element for 
, making it a unit ring
.
Given any set X, the power set of X forms a discrete ring of sets, while the collection {∅,X} constitutes the indiscrete ring of sets. Any field of sets and so also any σ-algebra also is a ring of sets.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nonempty collection of sets
is called a ring (of sets) if it is closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
. That is, for any
,
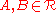where
represents the symmetric difference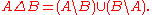A ring of sets forms an algebraic ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(possibly without unit) under these two operations. Intersection distributes over symmetric difference:
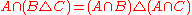
The empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is the identity element for
, and the union of all the sets, if it is in the ring, is the identity element for , making it a unit ringUnit ring
In mathematics, a unit ring or ring with a unit is a unital ring, i.e. a ring R with a multiplicative unit element, denoted by 1R or simply 1 if there is no risk of confusion.- Alternative definitions of a ring :...
.
Given any set X, the power set of X forms a discrete ring of sets, while the collection {∅,X} constitutes the indiscrete ring of sets. Any field of sets and so also any σ-algebra also is a ring of sets.