Motion graphs and derivatives
Encyclopedia
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the position vs. time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of an object is equal to the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the object. In the International System of Units
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
, the position of the moving object is measured in meters relative to the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, while the time is measured in second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s. Placing position on the y-axis and time on the x-axis, the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the curve is given by:
Here
is the position of the object, and 
is the time. Therefore, the slope of the curve gives the change in position (in metres) divided by the change in time (in seconds), which is the definition of the average velocity (in meters per second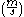 
) for that interval of time on the graph. If this interval is made to be infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
ly small, such that
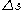becomes 
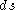and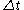 
becomes 
, the result is the instantaneous velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
at time
, or the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the position with respect to time.
A similar fact also holds true for the velocity vs. time graph. The slope of a velocity vs. time graph is acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, this time, placing velocity on the y-axis and time on the x-axis. Again the slope of a line is change in
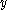over change in 
:
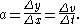
Where
is the velocity, measured in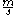 
, and 
is the time measured in seconds. This slope therefore defines the average acceleration over the interval, and reducing the interval infinitesimally gives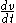 
, the instantaneous acceleration at time 
, or the derivative of the velocity with respect to time (or the second derivativeSecond derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
of the position with respect to time). The units of this slope or derivative are in meters per second per second
Metre per second squared
The metre per second squared is the unit of acceleration in the International System of Units . As a derived unit it is composed from the SI base units of length, the metre, and the standard unit of time, the second...
(
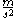, usually termed "meters per second-squared"), and so, therefore, is the acceleration.Since the velocity of the object is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the position graph, the area under the line
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
in the velocity vs. time graph is the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
of the object. (Velocity is on the y-axis and time on the x-axis. Multiplying the velocity by the time, the seconds cancel out and only meters remain.
.)The same multiplication rule holds true for acceleration vs. time graphs. When
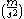is multiplied by time (s), velocity is obtained. (
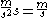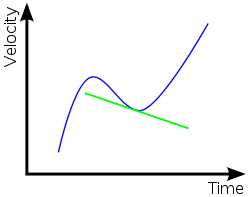
).Variable rates of change
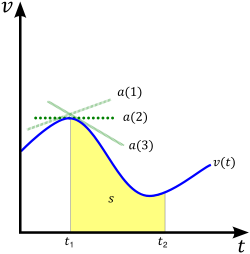
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
) rate of change is required. If the velocity or positions change non-linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
ly over time, such as in the example shown in the figure, then differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
provides the correct solution. Differentiation reduces the time-spans used above to be extremely small and gives a velocity or acceleration at each point on the graph rather than between a start and end point. The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
forms of the above equations are
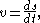
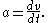
Since acceleration differentiates the expression involving position, it can be rewritten as a second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
with respect to position:
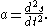
Since, for the purposes of mechanics such as this, integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is the opposite of differentiation, it is also possible to express position as a function of velocity and velocity as a function of acceleration. The process of determining the area under the curve, as described above, can give the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
and change in velocity over particular time intervals by using definite integrals:
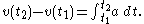
See also
- Displacement (vector)Displacement (vector)A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
- VelocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
- AccelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....