
Mountain pass theorem
Encyclopedia
The mountain pass theorem is an existence theorem
from the calculus of variations
. Given certain conditions on a function, the theorem demonstrates the existence of a saddle point
. The theorem is unusual in that there are many other theorems regarding the existence of extrema, but few regarding saddle points.
If we define: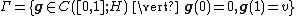
and: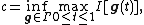
then the conclusion of the theorem is that c is a critical value of I.
 , and a far-off spot v where
, and a far-off spot v where 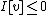 . In between the two lies a range of mountains (at
. In between the two lies a range of mountains (at 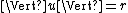 ) where the elevation is high (higher than a>0). In order to travel along a path g from the origin to v, we must pass over the mountains — that is, we must go up and then down. Since I is somewhat smooth, there must be a critical point somewhere in between. (Think along the lines of the mean-value theorem.) The mountain pass lies along the path that passes at the lowest elevation through the mountains. Note that this mountain pass is almost always a saddle point
) where the elevation is high (higher than a>0). In order to travel along a path g from the origin to v, we must pass over the mountains — that is, we must go up and then down. Since I is somewhat smooth, there must be a critical point somewhere in between. (Think along the lines of the mean-value theorem.) The mountain pass lies along the path that passes at the lowest elevation through the mountains. Note that this mountain pass is almost always a saddle point
.
For a proof, see section 8.5 of Evans.
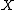 be Banach space
be Banach space
. The assumptions of the theorem are:
In this case there is a critical point
 of
of 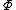 satisfying
satisfying 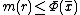 . Moreover if we define
. Moreover if we define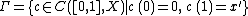
then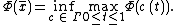
For a proof, see section 5.5 of Aubin and Ekeland.
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
from the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Given certain conditions on a function, the theorem demonstrates the existence of a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
. The theorem is unusual in that there are many other theorems regarding the existence of extrema, but few regarding saddle points.
Theorem statement
The assumptions of the theorem are:- I is a functionalFunctionalGenerally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
from a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H to the realsReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, -
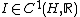 and
and 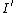 is Lipschitz continuous on bounded subsets of H,
is Lipschitz continuous on bounded subsets of H, - I satisfies the Palais-Smale compactness conditionPalais-Smale compactness conditionThe Palais–Smale compactness condition, named after Richard Palais and Stephen Smale, is a hypothesis for some theorems of the calculus of variations. It is useful for guaranteeing the existence of certain kinds of critical points, in particular saddle points...
, -
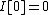 ,
, - there exist positive constants r and a such that
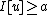 if
if 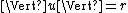 , and
, and - there exists
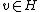 with
with 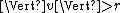 such that
such that 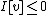 .
.
If we define:
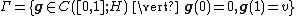
and:
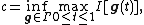
then the conclusion of the theorem is that c is a critical value of I.
Visualization
The intuition behind the theorem is in the name "mountain pass." Consider I as describing elevation. Then we know two low spots in the landscape: the origin because , and a far-off spot v where
, and a far-off spot v where 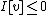 . In between the two lies a range of mountains (at
. In between the two lies a range of mountains (at 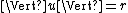 ) where the elevation is high (higher than a>0). In order to travel along a path g from the origin to v, we must pass over the mountains — that is, we must go up and then down. Since I is somewhat smooth, there must be a critical point somewhere in between. (Think along the lines of the mean-value theorem.) The mountain pass lies along the path that passes at the lowest elevation through the mountains. Note that this mountain pass is almost always a saddle point
) where the elevation is high (higher than a>0). In order to travel along a path g from the origin to v, we must pass over the mountains — that is, we must go up and then down. Since I is somewhat smooth, there must be a critical point somewhere in between. (Think along the lines of the mean-value theorem.) The mountain pass lies along the path that passes at the lowest elevation through the mountains. Note that this mountain pass is almost always a saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
.
For a proof, see section 8.5 of Evans.
Weaker formulation
Let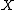 be Banach space
be Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The assumptions of the theorem are:
-
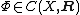 and have a Gâteaux derivativeGâteaux derivativeIn mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
and have a Gâteaux derivativeGâteaux derivativeIn mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
 which is continuous when
which is continuous when 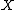 and
and 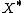 are endowed with strong topologyStrong topologyIn mathematics, a strong topology is a topology which is stronger than some other "default" topology. This term is used to describe different topologies depending on context, and it may refer to:* the final topology on the disjoint union...
are endowed with strong topologyStrong topologyIn mathematics, a strong topology is a topology which is stronger than some other "default" topology. This term is used to describe different topologies depending on context, and it may refer to:* the final topology on the disjoint union...
and weak* topology respectively. - There exists
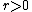 such that one can find certain
such that one can find certain 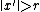 with
with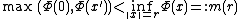 .
. -
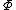 satisfies weak Palais-Smale condition on
satisfies weak Palais-Smale condition on 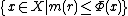 .
.
In this case there is a critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
 of
of 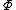 satisfying
satisfying 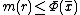 . Moreover if we define
. Moreover if we define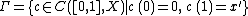
then
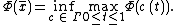
For a proof, see section 5.5 of Aubin and Ekeland.

