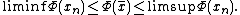Palais-Smale compactness condition
Encyclopedia
The Palais–Smale compactness condition, named after Richard Palais and Stephen Smale
, is a hypothesis for some theorems of the calculus of variations
. It is useful for guaranteeing the existence of certain kinds of critical point
s, in particular saddle point
s. The Palais-Smale condition is a condition on the functional
that one is trying to extremize.
In finite-dimensional spaces, the Palais–Smale condition for a continuously differentiable real-valued function is satisfied automatically for proper map
s: functions which do not take unbounded sets into bounded sets. In the calculus of variations, where one is typically interested in infinite-dimensional function space
s, the condition is necessary because some extra notion of compactness beyond simple boundedness is needed. See, for example, the proof of the mountain pass theorem
in section 8.5 of Evans.
functional
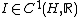 from a Hilbert space
from a Hilbert space
H to the reals
satisfies the Palais-Smale condition if every sequence
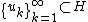 such that:
such that:
has a convergent subsequence in H.
and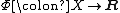 be a Gâteaux differentiable
be a Gâteaux differentiable
functional. The functional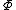 is said to satisfy the weak Palais-Smale condition if for each sequence
is said to satisfy the weak Palais-Smale condition if for each sequence 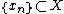 such that
such that
there exists a critical point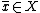 of
of 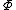 with
with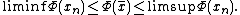
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
, is a hypothesis for some theorems of the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. It is useful for guaranteeing the existence of certain kinds of critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s, in particular saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
s. The Palais-Smale condition is a condition on the functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
that one is trying to extremize.
In finite-dimensional spaces, the Palais–Smale condition for a continuously differentiable real-valued function is satisfied automatically for proper map
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
s: functions which do not take unbounded sets into bounded sets. In the calculus of variations, where one is typically interested in infinite-dimensional function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, the condition is necessary because some extra notion of compactness beyond simple boundedness is needed. See, for example, the proof of the mountain pass theorem
Mountain pass theorem
The mountain pass theorem is an existence theorem from the calculus of variations. Given certain conditions on a function, the theorem demonstrates the existence of a saddle point...
in section 8.5 of Evans.
Strong formulation
A continuously Fréchet differentiableFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
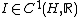 from a Hilbert space
from a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H to the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
satisfies the Palais-Smale condition if every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
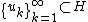 such that:
such that:
-
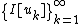 is bounded, and
is bounded, and -
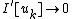 in H
in H
has a convergent subsequence in H.
Weak formulation
Let X be a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and
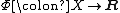 be a Gâteaux differentiable
be a Gâteaux differentiableGâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
functional. The functional
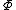 is said to satisfy the weak Palais-Smale condition if for each sequence
is said to satisfy the weak Palais-Smale condition if for each sequence 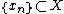 such that
such that
-
 ,
, -
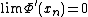 in
in 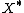 ,
, -
 for all
for all 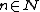 ,
,
there exists a critical point
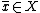 of
of  with
with