
Movable cellular automaton
Encyclopedia
The Movable cellular automaton (MCA) method is a method in computational solid mechanics
based on the discrete concept. It provides advantages both of classical cellular automaton
and discrete element
methods. Important advantage of the МСА method is a possibility of direct simulation
of materials fracture including damage generation, crack propagation, fragmentation and mass mixing. It is difficult to simulate these processes by means of continuum mechanics
methods (For example: finite element method
, finite difference method
, etc.), so some new concepts like peridynamics
is required. Discrete element method
is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. If size of automaton will be close to zero then MCA behavior becomes like classical continuum mechanics
methods.
The initial structure is formed by setting up certain relationships among each pair of neighboring elements.
So the changing of the state of pair relationships is controlled by relative movements of the automata and the media formed by such pairs can be considered as bistable media.
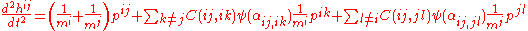
Here mi is the mass of automaton i, pij is central force acting between automata i and j, C(ij,ik) is certain coefficient associated with transferring the h parameter from pair ij to pair ik, ψ(αij,ik) is angle between directions ij and ik.
Due to finite size of movable automata the rotation effects have to be taken into account. The equations of motion for rotation can be written as follows:

Here Θij is the angle of relative rotation (it is a switching parameter like hij for translation), qij is the distance from center of automaton i to contact point of automaton j (moment arm), τij is the pair tangential interaction, S(ij,ik) is certain coefficient associated with transferring the Θ parameter from one pair to other (it is similar to C(ij,ik) from the equation for translation).
It should be noted that these equations are completely similar to the equations of motion for the many–particle approach.
The dimensionless deformation parameter for translation of the i j automata pair can be presented as:
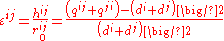
In this case:

where Δt time step, Vnij – relative velocity.
Rotation of the pair automata can be calculated by analogy with the last translation relationships.
As an example the titanium specimen under cyclic loading (tension – compression) is considered. The loading diagram is shown in the next figure:
Using boundary conditions of different types (fixed, elastic, viscous-elastic, etc.) it is possible to imitate different properties of surrounding medium, containing the simulated system. It is possible to model different modes of mechanical loading (tension, compression, shear strain, etc.) by setting up additional conditions at the boundaries.
Computational mechanics
Computational mechanics is the discipline concerned with the use of computational methods to study phenomena governed by the principles of mechanics. Before the emergence of computational science as a "third way" besides theoretical and experimental sciences, computational mechanics was widely...
based on the discrete concept. It provides advantages both of classical cellular automaton
Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
and discrete element
Discrete element method
A discrete element method , also called a distinct element method is any of family of numerical methods for computing the motion of a large number of particles of micrometre-scale size and above...
methods. Important advantage of the МСА method is a possibility of direct simulation
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
of materials fracture including damage generation, crack propagation, fragmentation and mass mixing. It is difficult to simulate these processes by means of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
methods (For example: finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
, etc.), so some new concepts like peridynamics
Peridynamics
Peridynamics is a formulation of continuum mechanics that is oriented toward deformations with discontinuities, especially fractures.-Purpose of peridynamics:...
is required. Discrete element method
Discrete element method
A discrete element method , also called a distinct element method is any of family of numerical methods for computing the motion of a large number of particles of micrometre-scale size and above...
is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. If size of automaton will be close to zero then MCA behavior becomes like classical continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
methods.
Keystone of the movable cellular automaton method
In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: Ri – radius-vector of automaton; Vi – velocity of automaton; ωi – rotation velocity of automaton; θi – rotation vector of automaton; mi – mass of automaton; Ji – moment of inertia of automaton.New concept: neighbours
The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.Definition of the parameter of pair state
The introducing of new type of states leads to new parameter to use it as criteria for switching relationships. It is defined as an automaton overlapping parameters hij. So the relationship of the cellular automata is characterised by the value of their overlapping.The initial structure is formed by setting up certain relationships among each pair of neighboring elements.
Criterion of switching of the state of pair relationships
In contrast to the classical cellular automaton method in the MCA method not only a single automaton but also a relationship of pair of automata can be switched. According with the bistable automata concept there are two types of the pair states (relationships):| linked | – both automata belong to a solid |
| unlinked | – each automaton of the pair belongs to different bodies or parts of damaged body. |
So the changing of the state of pair relationships is controlled by relative movements of the automata and the media formed by such pairs can be considered as bistable media.
Equations of MCA motion
The evolution of MCA media is described by the following equations of motion for translation: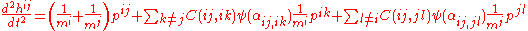
Here mi is the mass of automaton i, pij is central force acting between automata i and j, C(ij,ik) is certain coefficient associated with transferring the h parameter from pair ij to pair ik, ψ(αij,ik) is angle between directions ij and ik.
Due to finite size of movable automata the rotation effects have to be taken into account. The equations of motion for rotation can be written as follows:

Here Θij is the angle of relative rotation (it is a switching parameter like hij for translation), qij is the distance from center of automaton i to contact point of automaton j (moment arm), τij is the pair tangential interaction, S(ij,ik) is certain coefficient associated with transferring the Θ parameter from one pair to other (it is similar to C(ij,ik) from the equation for translation).
It should be noted that these equations are completely similar to the equations of motion for the many–particle approach.
Definition of deformation in pair of automata
Translation of the pair automataThe dimensionless deformation parameter for translation of the i j automata pair can be presented as:
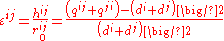
In this case:

where Δt time step, Vnij – relative velocity.
Rotation of the pair automata can be calculated by analogy with the last translation relationships.
Modeling of irreversible deformation in the MCA method
The εij parameter is used as a measure of deformation of automaton i under its interaction with automaton j. Where qij – is a distance from the center of automaton i to its contact point with automaton j; Ri = di/2 (di – is the size of automaton i).As an example the titanium specimen under cyclic loading (tension – compression) is considered. The loading diagram is shown in the next figure:
| Scheme of loading | Loading diagram |
|---|---|
| (Red marks are the experimental data) |
Advantages of MCA method
Due to mobility of each automaton the MCA method allows to take into account directly such actions as:- mass mixing
- penetration effects
- chemical reactions
- intensive deformation
- phase transformations
- accumulation of damages
- fragmentation and fracture
- cracks generation and development
Using boundary conditions of different types (fixed, elastic, viscous-elastic, etc.) it is possible to imitate different properties of surrounding medium, containing the simulated system. It is possible to model different modes of mechanical loading (tension, compression, shear strain, etc.) by setting up additional conditions at the boundaries.
Software
- MCA software package
- Software for simulation of materials in discrete-continuous approach «FEM+MCA»: Number of state registration in Applied Research Foundation of Algorithms and Software (AFAS): 50208802297 / Smolin A.Y., Zelepugin S.A., Dobrynin S.A.; applicant and development center is Tomsk State University. – register date 28.11.2008; certificate AFAS N 11826 date 01.12.2008.
See also
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
- Solid mechanicsSolid mechanicsSolid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
- PeridynamicsPeridynamicsPeridynamics is a formulation of continuum mechanics that is oriented toward deformations with discontinuities, especially fractures.-Purpose of peridynamics:...
- Computer simulationComputer simulationA computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
- Discrete element methodDiscrete element methodA discrete element method , also called a distinct element method is any of family of numerical methods for computing the motion of a large number of particles of micrometre-scale size and above...
- Cellular automatonCellular automatonA cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
- Finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
- Finite difference methodFinite difference methodIn mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...

